Метод квадратных корней

Введение

Система линейных алгебраических уравнений – математическая модель, которая описывает состояние равновесия экономического объекта, которое называется установившимся режимом или статикой объекта. Экономическая статика изучает допустимые и рациональные состояния экономического объекта.

Пусть дана система n линейных алгебраических уравнений с n неизвестными

(1.1)

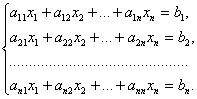
или в матричной форме

Ax = b,

где

- матрица коэффициентов,

- столбец свободных членов и столбец неизвестных соответственно.

Если матрица А неособенная, т.е.

то система (1.1) имеет единственное решение. В этом случае решение системы (1.1) с теоретической точки зрения не представляет труда. Значения неизвестных x_i (i=1,2,…n) могут быть получены по известным формулам Крамера

крамер квадратный корень матрица

где матрица A_i получается из матрицы А заменой ее i-го столбца столбцом свободных членов.

Но такой способ решения линейной системы с n неизвестными приводит к вычислению n + 1 определителей порядка n, что представляет собой весьма трудоемкую операцию при сколько-нибудь большом числе n.

Применяемые в настоящее время методы решения линейных систем можно разбить на две группы: точные и приближенные.

Точными методами называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), приводят к точным значениям неизвестных x_i. Так как на практике все вычисления ведутся с округлениями, то и значения неизвестных, полученные точным методом, неизбежно будут содержать погрешности. К точным методам относятся, например, метод Гаусса, метод квадратных корней.

Приближенными методами называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы (x₁, x₂, …, x_n) лишь с заданной точностью. Точное решение системы в этих случаях может быть получено теоретически как результат бесконечного процесса. К приближенным методам относятся метод простой итерации, метод Зейделя и др. Каждый из этих методов не всегда является сходящимся в применении к конкретному классу систем линейных уравнений.

Данная контрольная работа имеет следующую структуру: в начале рассматривается математическая постановка задачи для метода квадратных корней при решении систем линейных алгебраических уравнений. Затем производится реализация данного метода с помощью вычислительных средств ЭВМ, а именно прикладной программой Matlab 6.5. На примере реализации нескольких тестовых задач проводится анализ точности данного метода, а именно когда наиболее эффективно применять метод квадратных корней при решении систем линейных алгебраических уравнений. Анализ проводится на основе матрицы А (ее мерности, разреженности, обусловленности. Результаты, полученные на основе метода квадратных корней, приведены в конце данной работы. Также в работе представлен графический материал. По окончании проведения исследования работа завершается логическим заключением.

Математическая постановка задачи

 

Метод квадратных корней используется для решения линейной системы

Ax = b,

(1.2)

у которой матрица А симметрическая, т.е.

a_ij = a_ji (i, j = 1, 2, …, n).

Метод является более экономным и удобным по сравнению с решением систем общего вида.

Решение системы осуществляется в два этапа.

Прямой ход. Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц:

(1.3)

А = Т¢ Т,

где

.

Перемножая матрицы T¢ и T и приравнивая матрице A, получим следующие формулы для определения t_ij:

(1.4)

После того, как матрица Т найдена, систему (1.2) заменяем двумя эквивалентными ей системами с треугольными матрицами

	(1.5)

T¢y = b, Tx = y.

Обратный ход. Записываем в развернутом виде системы (1.5):

Отсюда последовательно находим

При вычислениях применяется обычный контроль с помощью сумм, причем при составлении суммы учитываются все коэффициенты соответствующей строки.

Заметим, что при действительных a_ij могут получиться чисто мнимые t_ij. Метод применим и в этом случае.

Описание программного обеспечения (согласно стандартам на ИТ)

Для изучения данного метода было выбрано программное обеспечение: Matlab 6.5, в операционной системе Windows XP Professional. На этапе проектирования была создана программа Square (‘квадрат^). Входными переменными для данной программы является матрица A и соответствующая ей матрица B. Результатом выполнения данной программы является матрица X (выходная переменная), которая является решением системы линейных алгебраических уравнений.

Ниже описан алгоритм реализации метода квадратных корней на языке программирования в среде Matlab 6.5:

A=input("Введите матрицу A=");

B=input("Введите B=");

if A==A"

if det(A)~=0

s=size(A,1);

if size(B",1) == s

T=zeros(s);

T(1,1)=sqrt(A(1,1));

for k=2:s

T(1,k)=A(1,k)/T(1,1)

end

for j=2:s

for i=2:s

if i==j

sm=0

for k=1:(i-1)

sm=sm+T(k,i)^2

end

T(i,i)=sqrt(A(i,i)-sm)

else

if i

sm=0

for k=1:(i-1)

sm=sm+T(k,i)*T(k,j)

end

T(i,j)=(A(i,j)-sm)/T(i,i)

end

end

end

end

Y=zeros(s,1)

Y(1)=B(1)/T(1,1)

for i=2:s

sm=0

for k=1:(i-1)

sm=sm+T(k,i)*Y(k)

end

sm

Y(i)=(B(i)-sm)/T(i,i)

end

X=zeros(s,1)

X(s)=Y(s)/T(s,s)

for m=1:(s-1)

i=s-m

sm=0

for k=(i+1):s

sm=sm+T(i,k)*X(k)

sm

end

X(i)=(Y(i)-sm)/T(i,i)

E=A*X-B"

end

else

error("B не соответствует матрице А")

end

else

error("det А = 0")

end

else

B = B*A"

A = A*A"

if det(A)~=0

s=size(A,1);

if size(B",1) == s

T=zeros(s);

T(1,1)=sqrt(A(1,1));

for k=2:s

T(1,k)=A(1,k)/T(1,1)

end

for j=2:s

for i=2:s

if i==j

sm=0

for k=1:(i-1)

sm=sm+T(k,i)^2

end

T(i,i)=sqrt(A(i,i)-sm)

else

if i

sm=0

for k=1:(i-1)

sm=sm+T(k,i)*T(k,j)

end

T(i,j)=(A(i,j)-sm)/T(i,i)

end

end

end

end

Y=zeros(s,1)

Y(1)=B(1)/T(1,1)

for i=2:s

sm=0

for k=1:(i-1)

sm=sm+T(k,i)*Y(k)

end

sm

Y(i)=(B(i)-sm)/T(i,i)

end

X=zeros(s,1)

X(s)=Y(s)/T(s,s)

for m=1:(s-1)

i=s-m

sm=0

for k=(i+1):s

sm=sm+T(i,k)*X(k)

sm

end

X(i)=(Y(i)-sm)/T(i,i)

end

else

error("B не соответствует матрице А")

end

else

error("det А = 0")

end

end

Описание тестовых задач

 

Результатом разработки программы является этап реализации и тестирования метода квадратных корней. На этапе выполнения программы может появляться неточность полученного решения из-за ошибки вычисления (например, ошибки округления ЭВМ). Исследуем влияние мерности матрицы A, ее обусловленности, разреженности на точность полученного решения. Результат будем оценивать по невязке ε = Ax^* - b (x^* - полученное решение). Для этого рассмотрим разного рода матрицы:

ü  влияние мерности матрицы А;

Рассмотрим матрицы мерности 2´2, 3´3, 4´4 и 5´5. Зададим матрицу мерностью 2´2:

, ей соответственно зададим , в результате выполнения программы получим решение:

X =

ε =

Зададим матрицу размерностью 3´3:

, ей соответственно зададим , в результате выполнения программы получим решение:

X =

ε =

Зададим матрицу размерностью 4´4:

, ей соответственно зададим , в результате выполнения программы получим решение:

X =

ε =

Зададим матрицу размерностью 5´5:

, ей соответственно зададим , в результате выполнения программы получим решение:

X =

ε =

Сравним полученные результаты, для этого проанализируем точность полученного решения. Результат мы можем оценить двумя способами  и , где E – матрица, полученная в результате подстановки найденного решения в систему линейных алгебраических уравнений: Е=A*x-b. Проиллюстрируем результаты графически. Для этого была разработана программа в среде Matlab 6.5.

E2=input("Введите матрицу Е2=");

E3=input("Введите матрицу Е3=");

E4=input("Введите матрицу Е4=");

E5=input("Введите матрицу Е5=");

Q1=sqrt(sum(power(E2,2)));

Q2=sqrt(sum(power(E3,2)));

Q3=sqrt(sum(power(E4,2)));

Q4=sqrt(sum(power(E5,2)));

Q = [Q1 Q2 Q3 Q4];

abs(E2);

abs(E3);

abs(E4);

abs(E5);

a1=max(abs(E2));

a2=max(abs(E3));

a3=max(abs(E4));

a4=max(abs(E5));

A = [a1 a2 a3 a4];

E = [2 3 4 5];

plot (Q,E)

pause

plot (A,E)

На основе проведенного анализа и иллюстрации графиков можно сделать вывод, что с увеличением мерности матрицы увеличивается неточность решения.

ü  влияние обусловленности матрицы А;

Для исследования возьмем матрицу следующего вида, которую в последствии будем заполнять нулями, прослеживая результат изменения ошибки:

, ей соответственно зададим

X =

-6.1000

-2.2000

-6.8000

-0.9000

0.2000

E =

-0.0389

-0.7994

0.2665

-0.0888

0.0888

, ей соответственно зададим

X =

-0.7869

-1.3706

-2.1805

-0.0204

1.5371

E =

0

0

0.2665

0

0

, ей соответственно зададим

X =

-0.4950

0.1575

5.0050

4.7700

-5.5025

E =

0

0

0

-0.7105

0.4441

, ей соответственно зададим

X =

-4.1125

1.0263

-1.0750

1.2947

-1.2313

E =

-0.0444

0

0.0888

-0.0888

0.1776

, ей соответственно зададим

X =

0.5000

1.0263

1.6667

1.2947

0.8250

E =

0

0

0.8882

-0.8882

0

Четкой тенденции проследить невозможно, хотя видно на основе предложенной матрицы А, что с увеличение числа нулей, присутствующих в матрице, точность решения увеличивается, т.к. уменьшается число элементов задействованных в вычислении, то и снижается ошибка вычислений.

ü  обусловленность матрицы А;

Зададим матрицу с практически равными элементами. В последствии будем увеличивать ее размерность.

, ей соответствует

X =

-1.6499

-1.6501

E =

0

-0.9313

, ей соответствует

X =

-1.6522

0.7500

2.3978

E =

0

0.1863

0

, ей соответствует

X =

0.0018

2.4041

2.3978

0.0033

E =

-0.0167

0.0371

-0.0371

-0.3558

Обусловленность матрицы снижает ошибку вычислений у матриц с более высокой размерностью, т.е. с увеличением размерности разряженной матрицы ее точность увеличивается (ошибка вычислений снижается).

Анализ результатов

 

Подводя итоги можно сделать следующий вывод. Точность решения зависит как от обусловленности, разреженности и мерности матрицы, так и в целом комбинация этих составляющих влияет на точность полученного решения. Хотя в некоторых случаях однозначного ответа дать невозможно, так как точность зависит еще и от того, насколько громоздки были вычисления, и как много требовалось округлений, а также все ли были учтены недочеты. А также если корни будут близки к целым корням, то и точность решения будет выше.

Заключение

 

В данной контрольной работе был проанализирован один из методов решения систем линейных алгебраических уравнений: метод квадратных корней. Метод был предложен для решения системы Ax=b, где матрица A – симметрическая, хотя не исключено, что метод может использоваться и не для симметрических матриц, тогда исходную систему можно привести к виду AA¢x=b A¢, полученную систему легко можно решить методом квадратных корней.

Также в данной системе были проанализированы разного рода матрицы, и их влияние на точность полученного решения. Основываясь на полученных выводах, можно контролировать в каких конкретно моментах удобно решать систему линейных алгебраических уравнений методом квадратных, а когда лучше использовать другой метод.

Литература

 

1.  Государственные стандарты. ИТ. комплекс стандартов и руководящих документов на АС. Издание официальное. Комплект стандартизации и метрологии СССР. М. – 1991.

2.  Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: «Наука», 1972.

3.  Писсанецки С. Технология разряженных матриц. – М.: Мир, 1988.

4.  Сарычева О.М. Численные методы в экономике: Конспект лекций. Новосибирск: НГТУ, 1995.

5.  Численные методы. Методические указания. НГТУ, 2002.