Економічна статистика

Описание:
Тип работы: контрольная работа
Визначення залежності між виробництвом продукції та собівартістю зернових за допомогою аналітичного групування. Обчислення загальних індексів та абсолютного приросту фізичного обсягу реалізації, цін, товарообороту за даними продовольчого магазину.
Доступные действия
Введите защитный код для скачивания файла и нажмите "Скачать файл"
Защитный код
Введите защитный код
Нажмите на изображение для генерации защитного кода

Текст:

Задача 1

За даними 25 підприємств за допомогою аналітичного групування з рівновеликими інтервалами (в три групи) прослідкувати залежність між виробництвом продукції та собівартістю зернових.

1.         Результати групування оформити в таблиці та детально проаналізувати.

2.         Оцінити суттєвість різниці середніх значень собівартості продукції по підприємствах першої та третьої груп за допомогою t-критерія Стьюдента.

Підприємства Вироблено продукції, тис. шт. Загальна сума витрат, тис. грн. Собівартість одиниці продукції, грн.
1 8,5 35 9,15
2 2,7 29 7,01
3 4,0 67 8,37
4 9,8 59 9,64
5 2,5 31 9,11
6 4,9 68 9,09
7 7,1 23 7,95
8 11,0 91 7,61
9 5,2 43 8,20
10 6,9 37 8,77
11 10,7 53 9,00
12 4,1 20 9,35
13 7,3 61 9,41
14 9,7 46 8,79
15 6,3 32 8,95
16 5,2 29 8,99
17 9,0 37 9,95
18 8,9 59 8,11
19 7,1 43 8,40
20 6,4 27 7,50
21 10,1 85 8,33
22 3,9 70 7,99
23 4,5 31 9,13
24 6,3 55 8,45
25 9,7 42 9,39

Рішення:

Проведемо угруповання за кількістю виготовленої продукції.

Для проведення групування визначимо інтервал групування:

,

де ,* - відповідно найбільше і найменше значення групувальної ознаки;

*       - кількість груп;

*        інтервал.

Отже інтервал групування дорівнює:

 

і = (11 – 2,5)/3 = 2,84

Відобразимо дані групування в таблицю:

№ п/п Вироблено продукції, тис. шт. Загальна сума витрат, тис. грн. Собівартість одиниці продукції, грн. Кількість підприємств
1 2,5 – 5,34 338 77,24 9
2 5,34 – 8,18 278 59,43 7
3 8,18 – 11,02 507 79,97 9

Для визначення тісноти зв^язку між кількістю виготовленої продукції і собівартістю продукції розрахуємо коефіцієнт кореляції:

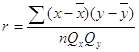
Для розрахунку потрібно визначити середнє квадратичне відхилення обох ознак, використовуючи формулу:

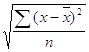
*=171/25 = 6,872

= 216,64/25 = 8,67

Дані розраховані за допомогою формули середньої звичайної:

Розрахуємо середнє квадратичне відхилення:

=  2,49

*= = 0,49

*8,3179/30,5 = 0,27

як показали розрахунки між кількістю виготовленої продукції і собівартістю одиниці продукції існує тісний зв^язок.

Проведемо оцінку суттєвості різниці середніх значень собівартості продукції по підприємствах першої та третьої груп за допомогою t-критерія Стьюдента. В таблиці наведено дані першої групи:

№ п/п Вироблено продукції, тис. шт. Собівартість одиниці продукції, грн.
1 2,5 9,11
2 2,7 7,01
3 3,9 7,99
4 4 8,37
5 4,1 9,35
6 4,5 9,13
7 4,9 9,09
8 5,2 8,2
9 5,2 8,99

Шляхом розрахунку середньої арифметичної звичайної середнє значення собівартості одиниці продукції дорівнює 8,58 грн. Дисперсія дорівнює 0,51, середнє квадратичне відхилення 0,72.

Знайдемо коефіцієнт варіації:

U = (0,72/8,58) * 100 = 8,39 %

t-критерій Стьюдента в даному випадку, для ступенів волі f = 9 – 1 = 8, і рівня довірчої імовірності 95 %, дорівнює 2,3060 таким чином довірчий інтервал для середнього значення дорівнює від 8,15 до 9,0.


Третя група має вигляд:

№ п/п Вироблено продукції, тис. шт. Собівартість одиниці продукції, грн.
1 8,5 9,15
2 8,9 8,11
3 9 9,95
4 9,7 8,79
5 9,7 9,39
6 9,8 9,64
7 10,1 8,33
8 10,7 9
9 11 7,61

Аналогічним чином знайдемо:

*=79,97/9 = 8,89

G2 = 4,5862/9 = 0,51

G = 0,71

U = (0,71/8,89) * 100 = 7,99

t-критерій Стьюдента в даному випадку, для ступенів волі f = 9 – 1 = 8, і рівня довірчої імовірності 95 %, дорівнює 2,36, таким чином довірчий інтервал для середнього значення дорівнює від 8,45 до 9,3.

Задача 2

За даними 25 підприємств побудувати ряд розподілу в 5 інтервалів (n = ) за загальною сумою витрат.

За рядом розподілу обчислити:

1.         Моду

2.         Медіану

3.         Зобразити графічно ряди розподілу: побудувати полігон та гістограму розподілу, огіву, кумуляту інтервального ряду розподілу.

Підприємства Вироблено продукції, тис. шт. Загальна сума витрат, тис. грн. Собівартість одиниці продукції, грн.
1 8,5 35 9,15
2 2,7 29 7,01
3 4,0 67 8,37
4 9,8 59 9,64
5 2,5 31 9,11
6 4,9 68 9,09
7 7,1 23 7,95
8 11,0 91 7,61
9 5,2 43 8,20
10 6,9 37 8,77
11 10,7 53 9,00
12 4,1 20 9,35
13 7,3 61 9,41
14 9,7 46 8,79
15 6,3 32 8,95
16 5,2 29 8,99
17 9,0 37 9,95
18 8,9 59 8,11
19 7,1 43 8,40
20 6,4 27 7,50
21 10,1 85 8,33
22 3,9 70 7,99
23 4,5 31 9,13
24 6,3 55 8,45
25 9,7 42 9,39

Рішення:

Для проведення групування визначимо інтервал групування за допомогою наступної формули:

,

де ,* - відповідно найбільше і найменше значення групувальної ознаки;

*       - кількість груп;

*        інтервал.

Отже інтервал групування дорівнює:

 

і = (91 – 20)/5 = 14,2

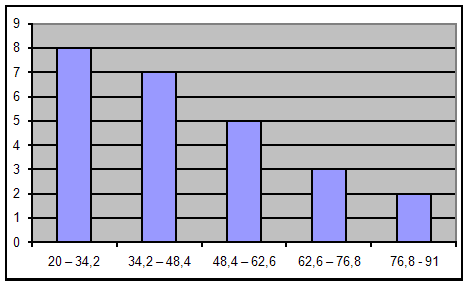
№ п/п Продуктивність праці Кількість заводів
1 20 – 34,2 8
2 34,2 – 48,4 7
3 48,4 – 62,6 5
4 62,6 – 76,8 3
5 76,8 - 91 2

Мода – це варіант, що частіше за все зустрічається в статистичному ряді. Мода розраховується за допомогою наступної формули:

Мо = х0 + і (fm – fm-1)/((fm – fm-1)(fm – fm+1))

де х0 – нижня границя модального інтервалу;

і – величина інтервалу;

fm – частота модального інтервалу;

fm-1 – частота інтервалу, що передує модальному інтервалу;

fm+1 – частота  наступного інтервалу за модальним інтервалом.

Проведемо відповідні розрахунки:

Мо = 20 + 14,2=20 + 14,2 * 0,067 = 20,95

Медіана розраховується за допомогою формули:

Ме = х0 + і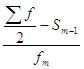

де (і Σf)/2 – сума всіх частот пополам;

Sm-1 – накопичена частота інтервалу, що передує медіанному;

fm – частота медіанного інтервалу.


Ме = 34,2 + 14,2 * ((12,5-8)/7) = 43,33

Побудуємо за даними групуваннями гістограму:

побудуємо полігон:


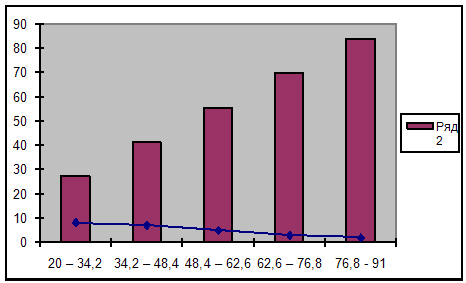
побудуємо кумулятивну криву:

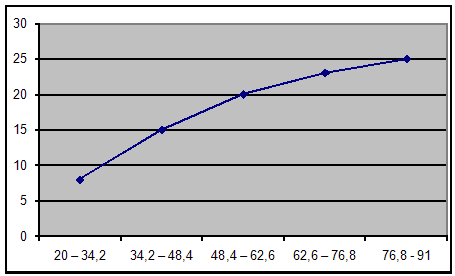
побудуємо огіву:


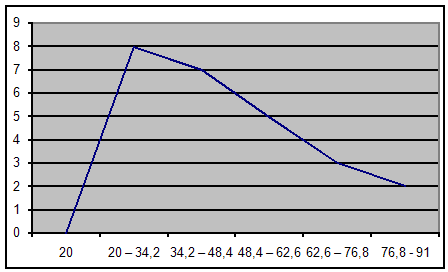
Задача 3

За даними 25 цехів заводів скласти і розв^язати рівняння кореляційної залежності виробництва литва на одного робітника і собівартістю 1 т, обчисливши при цьому ці показники для кожного заводу. Обчислити коефіцієнт кореляції. Побудувати графік кореляційної залежності. Зробити короткі висновки. Обчислення оформити в таблиці.

№ п/п заводів Виробництво литва на одного працівника, т Брак, % Собівартість 1 т, грн.
1 14,6 4,2 239
2 13,5 6,7 254
3 21,6 5,5 262
4 17,4 7,7 251
5 44,8 1,2 158
6 111,9 2,2 101
7 20,1 8,4 259
8 28,1 1,4 186
9 22,3 4,2 204
10 25,3 0,9 198
11 56,0 1,3 170
12 40,2 1,8 173
13 40,6 3,3 197
14 75,8 3,4 172
15 27,6 1,1 201
16 88,4 0,1 130
17 16,6 4,1 251
18 33,4 2,3 195
19 17,0 9,3 282
20 33,1 3,3 196
21 30,1 3,5 186
22 65,2 1,0 176
23 22,6 5,2 238
24 33,4 2,3 204
25 19,7 2,7 205

Рішення:

Для вияву і тісноти взаємозв^язку між показниками використаємо кореляційно - регресійні методи аналізу. Основною ціллю нашого аналізу є отримання апроксимуючої функції:

що найбільш реально відображає зв^язок між показниками, що вивчаються.

Для побудови одно факторної моделі розглянемо:

або

Параметри розраховуються по методу найменших квадратів, тобто коли система нормативних рівнянь при вирівнюванні має вигляд:

звідси

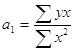
Розрахункові дані наведені в таблиці:

№ п/п заводів Виробництво литва на одного працівника, т (х) Собівартість 1 т, грн. (у) ху

х2
1 14,6 239 3489,4 57121
2 13,5 254 3429 64516
3 21,6 262 5659,2 68644
4 17,4 251 4367,4 63001
5 44,8 158 7078,4 24964
6 111,9 101 11301,9 10201
7 20,1 259 5205,9 67081
8 28,1 186 5226,6 34596
9 22,3 204 4549,2 41616
10 25,3 198 5009,4 39204
11 56,0 170 9520 28900
12 40,2 173 6954,6 29929
13 40,6 197 7998,2 38809
14 75,8 172 13037,6 29584
15 27,6 201 5547,6 40401
16 88,4 130 11492 16900
17 16,6 251 4166,6 63001
18 33,4 195 6513 38025
19 17,0 282 4794 79524
20 33,1 196 6487,6 38416
21 30,1 186 5598,6 34596
22 65,2 176 11475,2 30976
23 22,6 238 5378,8 56644
24 33,4 204 6813,6 41616
25 19,7 205 4038,5 42025
Всього 919,3 5088 165132,3 1080290

 919,3/25 = 36,772

*1651323/1080290 = 0,153

таким чином рівняння кореляційної залежності має вигляд:

* = 36,772 + 0,153 х

знайдемо коефіцієнт кореляції:

для цього визначимо середнє квадратне відхилення показників х і y:

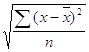
Розрахуємо середні показники виробництва литва на одного працівника і собівартості однієї тони продукції:

*=919,3/25 = 36,77

= 5088/25 = 203,52

Розрахунки оформимо в таблиці:



№ п/п заводів

1 -22,17 35,48 491,5089 1258,8304 -786,5916
2 -23,27 50,48 541,4929 2548,2304 -1174,6696
3 -15,17 58,48 230,1289 3419,9104 -887,1416
4 -19,37 47,48 375,1969 2254,3504 -919,6876
5 8,03 -45,52 64,4809 2072,0704 -365,5256
6 75,13 -102,52 5644,5169 10510,3504 -7702,3276
7 -16,67 55,48 277,8889 3078,0304 -924,8516
8 -8,67 -17,52 75,1689 306,9504 151,8984
9 -14,47 0,48 209,3809 0,2304 -6,9456
10 -11,47 -5,52 131,5609 30,4704 63,3144
11 19,23 -33,52 369,7929 1123,5904 -644,5896
12 3,43 -30,52 11,7649 931,4704 -104,6836
13 3,83 -6,52 14,6689 42,5104 -24,9716
14 39,03 -31,52 1523,3409 993,5104 -1230,2256
15 -9,17 -2,52 84,0889 6,3504 23,1084
16 51,63 -73,52 2665,6569 5405,1904 -3795,8376
17 -20,17 47,48 406,8289 2254,3504 -957,6716
18 -3,37 -8,52 11,3569 72,5904 28,7124
19 -19,77 78,48 390,8529 6159,1104 -1551,5496
20 -3,67 -7,52 13,4689 56,5504 27,5984
21 -6,67 -17,52 44,4889 306,9504 116,8584
22 28,43 -27,52 808,2649 757,3504 -782,3936
23 -14,17 34,48 200,7889 1188,8704 -488,5816
24 -3,37 0,48 11,3569 0,2304 -1,6176
25 -17,07 1,48 291,3849 2,1904 -25,2636
Всього 14889,4305 44780,24 -21963,636

= 24,4

*= = 42,32

Для розрахунку коефіцієнта кореляції використовується формула:

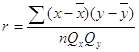
r = (-21963,636)/25815,2 = - 0,85

Оскільки коефіцієнт кореляції дорівнює показнику меншому за 0,3, то це свідчить про слабкий кореляційний зв^язок між параметрами, що аналізуються.

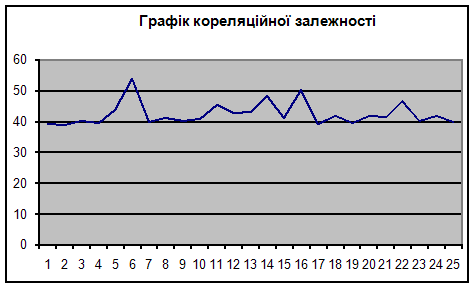
Побудуємо графік кореляційної залежності:

Задача 4

Товарооборот продовольчого магазину по основних групах товарів становив:

Назва продукту

 Товарооборот у поточних цінах, тис. грн. Зміни кількості продукції у звітному періоді порівняно з базисним, %
базисний звітний
М^ясо 35 50 +12
Молоко 46 46 +7
Овочі 35 55 -10

Обчислити:

1.         Обчислити загальні індекси та абсолютні прирости фізичного обсягу реалізації, цін, товарообороту.

2.         Показники взаємозв^язку між ними.

3.         Зробити короткі висновки.

 

Рішення:

Товарооберт, це рух товарної маси від виробника до споживача шляхом купівлі – продажу, шляхом обміну товару на гроші.

Взаємозв^язок між ціною (р) і кількістю проданих товарів (q) можна виразити через об^єм товарооберту, що дорівнює:

у випадку коли за період, що розглядається товар продавався і покупався кілька разів, то вартість цього товару стільки ж раз буде враховуватись в об^ємі товарообету.

Динаміка товарооберту вивчається в поточних цінах і спів ставних, загальний індекс товар оберту розраховується за допомогою формули:

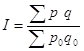
де I – загальний індекс товароберту;

p0p – ціни в базисному і звітному періоді відповідно;

q0 q – об^єм виготовленої продукції у базисному і звітному періоді.

І = 151/116 = 1,3 або 130 %

Абсолютний приріст = 151 – 116 = 35 тис.грн..

Таким чином товарооберт у звітному періоді збільшився на 35 тис. грн.. в порівнянні з базисним.

Виходячи з даних наведених у таблиці кількість м^ясної продукції в звітному періоді відносно базисного зросла на 12 %, отже індекс фізичного об^єму м^ясної продукції склав 1,12 або 112 %, при цьому виходячи з залежності, індекс цін дорівнює 0,013, або 1,3 %. Аналогічно індекс фізичного об^єму молочних продуктів склав 107 %, при цьому індекс ціни 0,0093, або 0,93 %. Обсяг продажу овочів знизився на 10 %, отже індекс фізичного об^єму продажу овочів склав 90 % або 0,9, при цьому індекс ціни на овочі склав 0,018 або 1,8 %.


Задача 5

Є дані про динаміку валового виробництва продукції, тис. т.

Роки Валовий збір, тис. т Базисні показники динаміки
Абсолютний приріст, тис. т Темп зростання, % Темп приросту, % Абсолютне значення 1 % приросту, тис. т
1997 132,8
1998 134,85 2,85 2,05 1,05 2,71
1999 929,6 796,8 7,0 6,0 132,8
2000 9827,2 9694,4 74,0 73,0 132,8
2001 796,8 664 6 5,0 132,8
2002 13678,4 13545,6 103,0 102,0 132,8
2003 398,4 265,6 3,0 2,0 132,8

Використовуючи взаємозв^язок показників динаміки, визначити рівні та показники, що відсутні в таблиці.

Рішення:

Оскільки абсолютний приріст валового виробництва продукції визначається, як відношення між двома рівнями ряду:

,

то знайдемо показник валового збору продукції в 1998 році:

 = 2,85 + 132 = 134,85

у відповідності до формули знайдемо темп зростання:


Т1998 = 134,85/132,8 = 2,05

Темп приросту знаходиться за формулою:

ΔТ = Тб – 1

ΔТ1998 = 2,05 – 1 = 1,05

Абсолютне значення приросту розраховується за допомогою наступної формули:

λ = Δ/ΔТ

λ = 2,85/1,05 = 2,71

тобто 2,71 є абсолютною величиною одного проценту приросту валового збору виробництва.

Шляхом математичних розрахунків, через вказані формули і підстановки відомих показників з таблиці, розрахуємо і занесемо до таблиці невідомі елементи, використовуючи базисний метод розрахунків.

Информация о файле
Название файла Економічна статистика от пользователя z3rg
Дата добавления 6.1.2012, 13:05
Дата обновления 6.1.2012, 13:05
Тип файла Тип файла (zip - application/zip)
Скриншот Не доступно
Статистика
Размер файла 55.92 килобайт (Примерное время скачивания)
Просмотров 877
Скачиваний 258
Оценить файл