РАСЧЕТ СПЕКТРА ОДИНОЧНОГО НЕПЕРИОДИЧЕСКОГО ВИДЕОИМПУЛЬСА

Оглавление

ВВЕДЕНИЕ.. 4

Задачи курсовой работы.. 5

Классификация и свойства сигналов. 5

Спектральные характеристики периодических сигналов. 7

Спектральные характеристики непериодического сигнала. 9

Свойства преобразования Фурье. 9

ГЛАВА 1. РАСЧЕТ СПЕКТРА ОДИНОЧНОГО НЕПЕРИОДИЧЕСКОГО ВИДЕОИМПУЛЬСА.. 13

Гармонический спектральный анализ непериодических сигналов. 13

Расчёт заданного одиночного видеоимпульса. 13

ГЛАВА 2. РАСЧЁТ СПЕКТРА ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ВИДЕОИМПУЛЬСОВ.. 17

Гармонический спектральный анализ периодических сигналов. 17

Расчет. 19

ГЛАВА 3. РАСЧЁТ СПЕКТРА ОДИНОЧНОГО НЕПЕРИОДИЧЕСКОГО РАДИОИМПУЛЬСА.. 22

Спектральный анализ амплитудно-модулированного сигнала. 22

Расчет. 22

ГЛАВА 4. РАСЧЁТ СПЕКТРА ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ РАДИОИМПУЛЬСОВ.. 25

Спектральный анализ амплитудно-модулированного сигнала. 25

Расчет. 25

ЗАКЛЮЧЕНИЕ.. 27

ВВЕДЕНИЕ

К числу важных областей науки и техники, достижения которых непосредственно способствуют росту материального и культурного уровня общества, принадлежит радиотехника.

Радиотехника – это область науки и техники, связанная с практическим использованием электромагнитных колебаний для передачи, извлечения, хранения и преобразования информации.

С этой целью изучаются теоретические и практические основы формирования (генерации), преобразования, передачи и приема электромагнитных колебаний радиочастотного диапазона. Изучение принципов генерации, усиления, излучения и приема электромагнитных колебаний и волн, относящихся к радиодиапазону.

Радиотехника нашла применение в различных областях науки, таких как физика,астрономия,медицина,химия. Радиотехнические методы применяются в системах передачи данных, радиосвязи, радиовещании, телевидении, радиолокации, радионавигации, радиоуправлении, системах автоматики и вычислительной техники.

Развитие радиотехники тесно связано с достижениями в области радиофизики,электроники, физики полупроводников, электроакустики, теории колебаний, теории информации (Информации теория), и различных разделах математики, а также с прогрессом в технике высокочастотных измерений (Измерительная техника, Радиоизмерения), вакуумной и полупроводниковой технике (Полупроводниковая электроника),в производстве источников электропитания и др. В Р. входит ряд областей, главные из которых — генерирование электрических колебаний, усиление электрических колебаний, их преобразование, управление ими (Модуляция колебаний), антенная техника (Антенна, Излучение и приём радиоволн), распространение радиоволн в свободном пространстве, в различных средах (ионосфере, почве) и в направляющих системах (кабелях, волноводах), фильтрация электромагнитных колебаний, демодуляция, воспроизведение переданных сигналов (речи, музыки, изображений, телеграфных и иных знаков), контроль, управление и регулирование при помощи ЭВ и колебаний (посредством радиоэлектронных систем).

В наши дни радиотехника является бурно развивающейся научно-прикладной областью. Говоря о ближайших перспективах ее развития, следует подчеркнуть тенденцию перехода к все более высокочастотным диапазонам электромагнитных колебаний и волн. Так, колебания сверхвысокочастотного (СВЧ) диапазона, ранее применявшиеся в основном в радиолокации, стали широко использоваться в телевизионных, связных и телеметрических радиоканалах. Достигнуты большие успехи в создании лазерных линий связи с несущими частотами, лежащими в световом и инфракрасном диапазонах.

Быстрыми темпами развивается элементная база радиотехники и радиоэлектроники. Если традиционные радиотехнические цепи представляли собой почти исключительно комбинации линейных и нелинейных электрических цепей, то сейчас интенсивно исследуются и внедряются в практику функциональные устройства и системы, производящие обработку сигналов за счет специфических волновых и колебательных явлений в твердых телах — полупроводниках, диэлектриках и магнитных материалах. Огромную роль в современной радиотехнике играют изделия микроэлектронной технологии.  Микроэлектроника обусловила широкий переход к принципиально новым цифровым способам обработки и преобразования радиотехнических сигналов.

Отрасли радиотехники будут и впредь расширяться и развиваться на базе прогресса во многих смежных областях науки и техники.

Задачи курсовой работы

Задачи данной курсовой работы:

- выполнить расчёт спектра одиночного непериодического видеосигнала;

- выполнить расчёт спектра периодической последовательности видеосигнала;

- выполнить расчёт спектра одиночного непериодического радиосигнала;

- выполнить расчёт спектра периодической последовательности радиосигнала;

Классификация и свойства сигналов

Классификация сигналов осуществляется на основании существенных признаков соответствующих математических моделей сигналов. Все сигналы разделяют на две крупных группы: детерминированные и случайные

 

Детерминированные сигналы–это сигналы, мгновенные значения которых в любой момент времени известны, т.е. предсказуемы с вероятностью, равной единице. Они могут быть описаны определенными функциями времени. Анализ и исследование этих сигналов осуществляется с помощью математического аппарата, не связанного с теорией вероятностей.

Периодические сигналы –это сигналы, которые можно представить функцией времени, удовлетворяющей условию

s(t) = s(t + nT),

 где n =...,-2,-1,0,1,2,... ; Т - период сигнала. Пример периодического сигнала - гармоническое колебание.

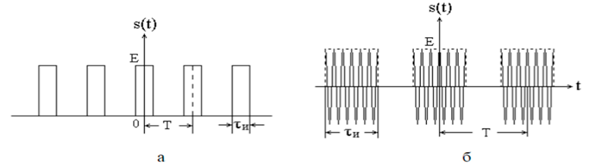
Рис.(а,б)Периодические сигналы

На практике наиболее часто встречаются периодические последовательно-сти видеоимпульсов (рис.а) и радиоимпульсов (рис.б).Такие последова-тельностив общем виде представляют формулой

  

Любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте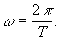

Непериодический сигнал, как правило, ограничен во времени.

Случайные сигналы–это сигналы, мгновенные значения которых в любой момент времени не известны, но могут быть предсказаны с вероятностью, меньшей единицы. Случайные сигналы являются объектом исследования статистической радиотехники, базирующейся на теории вероятностей, в частности на теории случайных процессов.

В качестве основных характеристик сигналов принимают:

1) Среднее значение сигнала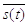

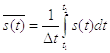, где - интервал времени на котором определен сигнал

2) Мгновенная мощность сигнала

3) Энергия сигнала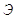

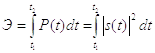
4) Средняя мощность сигнала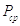

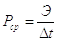
Для периодических сигналов данные характеристики рассматривают в пределах одного периода.

Спектральные характеристики периодических сигналов

Для упрощения методов решения задач анализа цепей сигналы представляют в виде суммы определенных функций.

Этот процесс обосновывается понятием обобщенного ряда Фурье. В математике доказано, что любая функция, удовлетворяющая условиям Дирихле, может быть представлена в виде ряда:

.

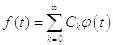Для определения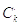 умножим левую и правую части ряда на 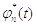 и возьмем интеграл от левой и правой части:

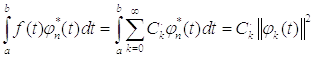, для интервала [a;b] в котором выполняются условия ортогональности.

Видно, что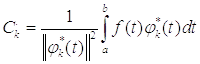.Получили выражение для обобщенного ряда Фурье:

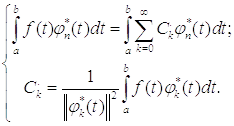
Выделим конкретный вид функции 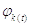, для разложения в ряд сигнала 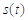. В качестве такой функции выберем ортогональную систему функций:

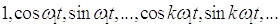
Для определения ряда вычислим значение :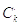

.

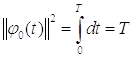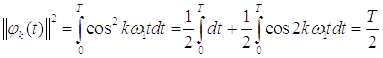, так как .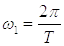

Таким образом, получим:

,

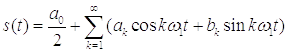где.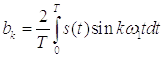

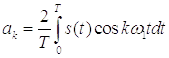Графически данный ряд представляется в виде двух графиков амплитудных гармонических составляющих.

Полученное выражение можно представить в ви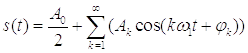де:

, где; .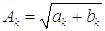

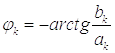Получили вторую форму записи тригонометрического ряда Фурье. Графически данный ряд представляется в виде двух графиков - амплитудного и фазового спектров.

Найдем комплексную форму ряда Фурье, для этого воспользуемся формулами Эйлера:

;

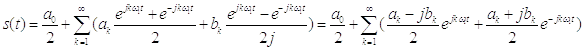,или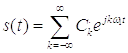, где

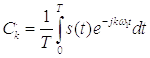
Графически спектр в этой форме представлен на оси частот в диапазоне.

Очевидно, что спектр периодического сигнала, выраженный в комплексной или амплитудной форме – дискретный. Это значит, что в спектре имеются составляющие с частотами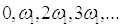

 Спектральные характеристики непериодического сигнала

    Так как в качестве непериодического сигнала в радиотехнике рассматривают одиночный сигнал, то для нахождения его спектра представим сигнал как периодический с периодом стремящимся к бесконечности. Воспользуемся преобразование ряда Фурье для данного периода. Получим для: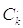

.

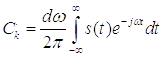Анализ полученного выражения показывает, что при 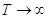амплитуды составляющих становятся бесконечно малыми и на оси частот они расположены непрерывно. Тогда, что б выйти из этого положения воспользуемся понятием спектральной плотности:

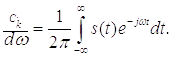
Подставим полученное выражение в комплексный ряд Фурье, получим:

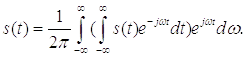
Окончательно получим:

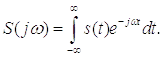
Здесь 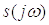- спектральная плотность, а само выражение – прямое преобразование Фурье. Для определения сигнала по его спектру используют обратное преобразование Фурье:

 Свойства преобразования Фурье

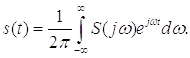
Из формул прямого и обратного преобразований Фурье, очевидно, что если изменится сигнал, то изменится и его спектр. Следующие свойства устанавливают зависимость спектра измененного сигнала, от спектра сигнала до изменений. 

1) Свойство линейности преобразования Фурье

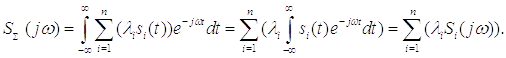, т.е.

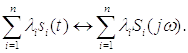
Получили, что спектр суммы сигналов равен сумме их спектров.

2) Спектр сигнала сдвинутого во времени

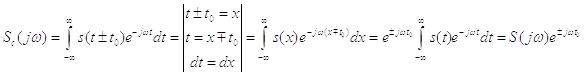
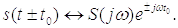
Получили, что при сдвиге сигнала амплитудный спектр не изменяется, а изменяется только фазовый спектр на величину .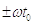

3) Изменение масштаба времени

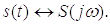
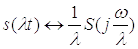т.е при расширении(сужении) сигнала в несколько раз спектр этого сигнала сужается(расширяется).

4) Спектр производной от сигнала

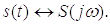
Возьмем производную от левой и правой части обратного преобразования Фурье.

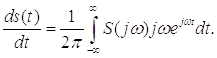
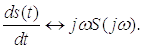
Видим, что спектр производной от сигнала равен спектру исходного сигнала умноженного на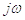, то есть изменяется амплитудный спектр и меняется фазовый на.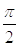

5) Спектр интеграла сигнала

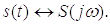
Возьмем интеграл от левой и правой части обратного преобразования Фурье.

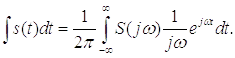
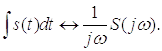
Видим, что спектр производной от сигнала равен спектру исходного сигнала деленного на,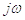

6) Спектр произведения двух сигналов

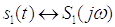
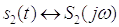
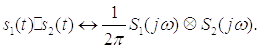
Таким образом, спектр произведения двух сигналов равен свертке их спектров умноженной на коэффициент.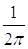

7) Свойство дуальности

;

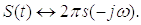
Таким образом, если к какому-то сигналу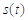 соответствует спектр 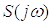, то сигналу по форме совпадающему с вышеуказанным спектром соответствует спектр по форме совпадающий с вышеуказанным сигналом.

ГЛАВА 1. РАСЧЕТ СПЕКТРА ОДИНОЧНОГО НЕПЕРИОДИЧЕСКОГО ВИДЕОИМПУЛЬСА Гармонический спектральный анализ непериодических сигналов

В радиотехнике в качестве непериодических сигналов рассматриваются периодические и периодом стремящимся к бесконечности.

Основные выражения для получения спектральных характеристик непериодических сигналов:

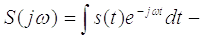Прямое преобразование Фурье (Спектральная плотность).

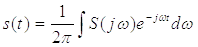- Обратное преобразование Фурье.

Амплитудный и фазовый спектры непериодического сигнала

Для спектральной плотности справедливы все свойства комплексных чисел:

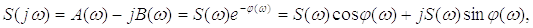
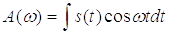 - действительная часть спектра;

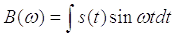- мнимая часть спектра;

- амплитудный спектр сигнала;

- фазовый спектр сигнала;

Расчёт заданного одиночного видеоимпульса

Графическое изображение непериодического видеоимпульса отображено на рисунке 1.

Данные для расчёта:

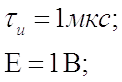
Сигнал:

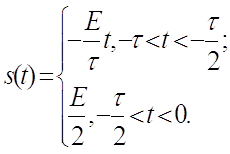
Расчёт прямым преобразование Фурье:

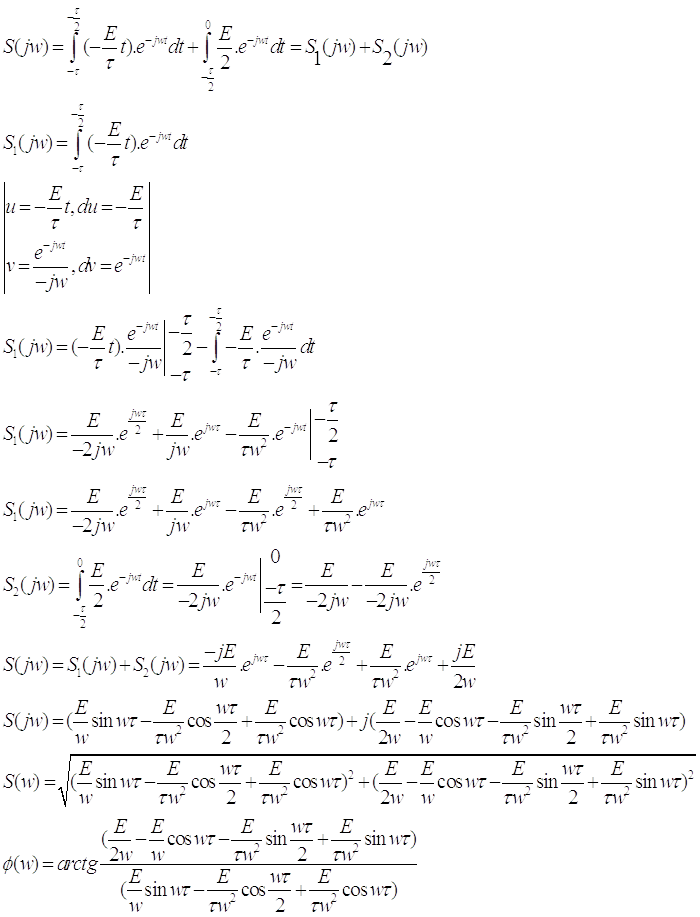
Для построения графиков воспользуемся программой MatLab. Полученные графики амплитудного и фазового спектра представлены на рисунке 2 и рисунке 3 соответственно.

ГЛАВА 2. РАСЧЁТ СПЕКТРА ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ВИДЕОИМПУЛЬСОВ Гармонический спектральный анализ периодических сигналов

Для определения частотных характеристик периодических сигналов, т.е

для их спектрального анализа, сигналы представляются в виде суммы гармонических колебаний путем разложения в ряд Фурье. Такое разложение существует, так как большинство применяемых на практике сигналов описывается функциями времени, удовлетворяющими условиям Дирихле: наличие конечного числа разрывов первого рода (скачков) и отсутствие разрывов второго рода (ветвей, уходящих в бесконечность), а также наличие конечного числа экстремумов.

Представление периодических сигналов в виде суммы гармонических колебаний с различными параметрами (прежде всего различными частотами) называют спектральным разложением или гармоническим спектральным анализом сигналов. Математически спектральный анализ предполагает разложение сигналов в ряд по тригонометрическим функциям – синусам и косинусам. Эти функции описывают гармонические колебания, которые сохраняют свою форму в процессе преобразований линейными устройствами (изменяются только амплитуда и фаза), что позволяет использовать теорию колебательных систем для анализа свойств радиотехнических цепей. Совокупность гармонических компонент образует спектр сигнала.

1) Тригонометрическая форма ряда Фурье.

Тригонометрическая форма ряда Фурье имеет вид:

,

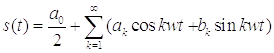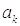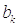Коэффициенты  и  этого ряда определяются выражениями:

                  ;                .

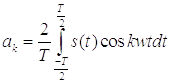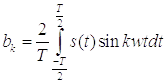Частота 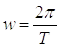, где T – период сигнала.

Практическое применение имеет другая форма записи тригонометрического ряда Фурье:

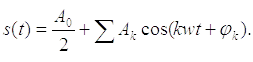
Получение такого ряда Фурье основано на известном преобразовании:

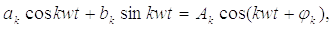
где 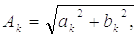  и  

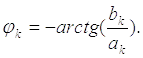
Совокупность составляющей 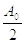и амплитуд 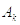 называют амплитудным спктром,а совокупность фаз  - фазовым спектром сигнала.

2) Комплексная форма ряда Фурье.

Комплексная форма ряда Фурье имеет вид:

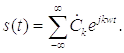
         Получение такого ряда Фурье основано на преобразовании тригонометрической формы ряда с использованием формул Эйлера:

;                              .

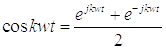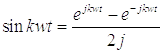Коэффициенты 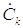 являются комплексными амплитудами k-х гармонических составляющих, oни определяются выражением:

,

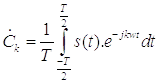Причем 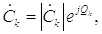где ,.

Расчет

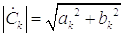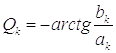Графическое изображение периодической последовательности видеоимпульсов отображено на рисунке 4.

Данные для расчёта:

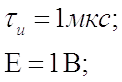
Сигнал:

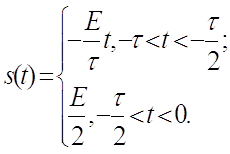
Заметив схожесть расчёта периодической последовательности видеоимпульсов и непериодического видеоимпульса можем записать:

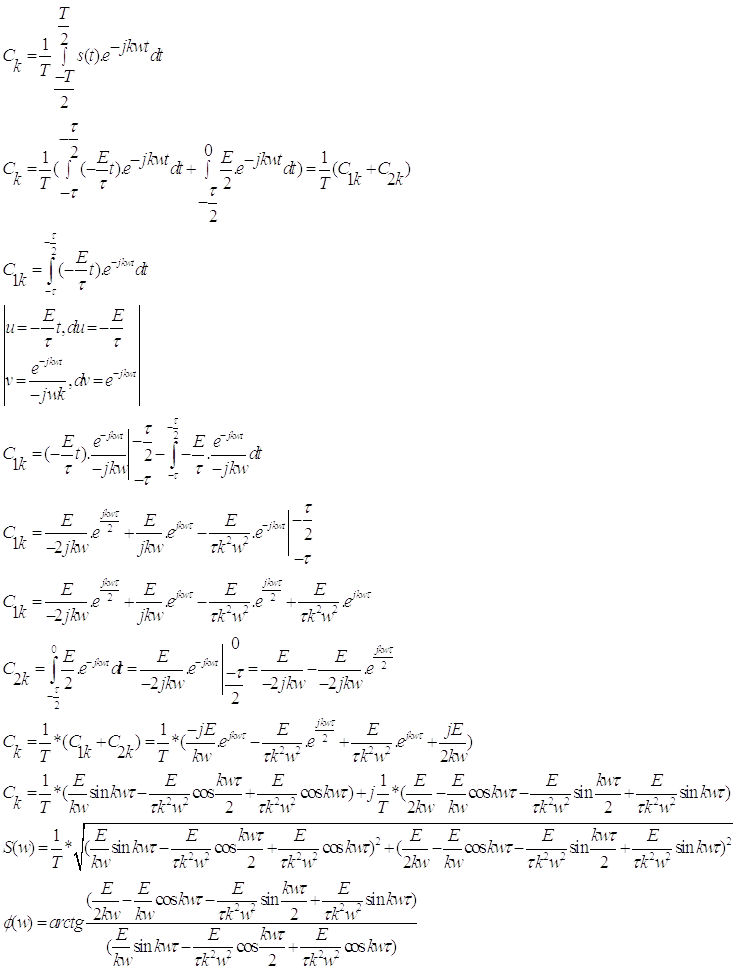
Для построения графиков воспользуемся программой MatLab. Полученные графики спектра амплитуд и спектра фаз представлены на рисунке 5 и рисунке 6 соответственно.

ГЛАВА 3. РАСЧЁТ СПЕКТРА ОДИНОЧНОГО НЕПЕРИОДИЧЕСКОГО РАДИОИМПУЛЬСА  Спектральный анализ амплитудно-модулированного сигнала

Радиоимпульс формируетсяв результате процесса амплитудной модуляции высокочастотного гармонического несущего колебания 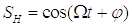импульсным сигналом (видеоимпульсом) .В результате образуется гармонический сигнал 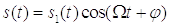,в котором  при соблюдении некоторых условий является огибающей.

Определим спектральную плотность сигнала s(t):

Расчет

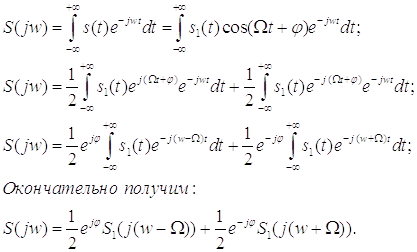
Одиночный непериодический радиоимпульс представлен на рисунке 7 в приложении 2.

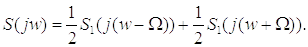
Данные для расчёта:

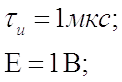
Сигнал:

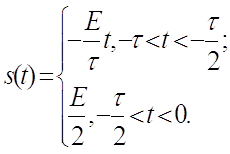
Используя результаты расчетов в главе 1, получим:

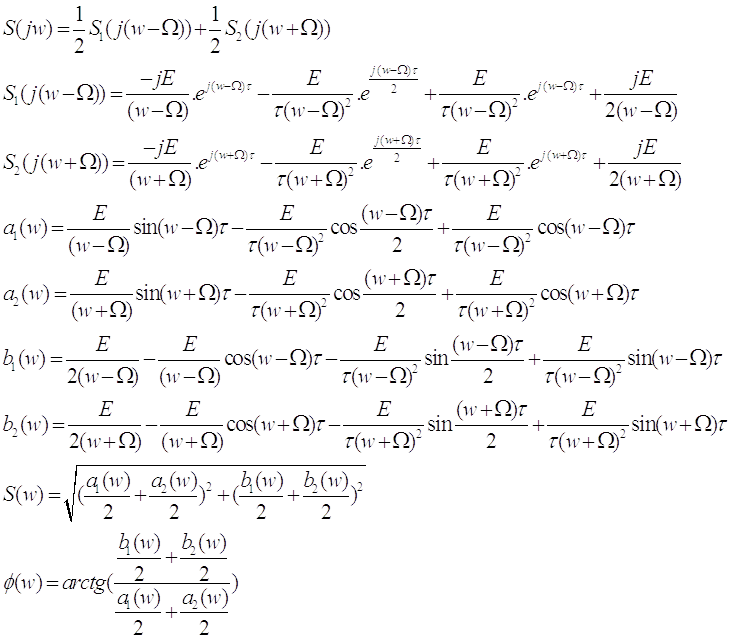
Для построения графиков воспользуемся программой MatLab. Полученные графики амплитудного и фазового спектров представлены на рисунке 8 и рисунке 9 соответственно.

ГЛАВА 4. РАСЧЁТ СПЕКТРА ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ РАДИОИМПУЛЬСОВ Спектральный анализ амплитудно-модулированного сигнала

Имеем:

Расчет

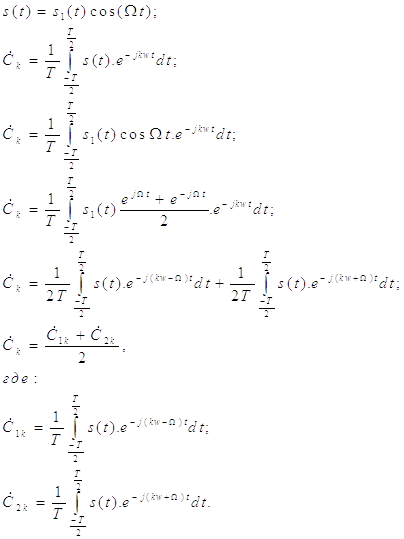
Графическое изображение периодической последовательности радиоимпульсов отображено на рисунке 10.

Данные для расчёта:

Данные для расчёта:

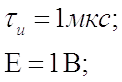
Сигнал:

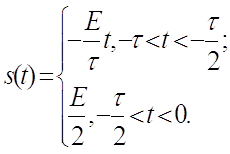
Используя результаты расчетов в главе 1, получим:

Для построения графиков воспользуемся программой MatLab. Полученные графики спектра амплитуд и спектра фаз представлены на рисунке 11 и рисунке 12 соответственно.

ЗАКЛЮЧЕНИЕ

В данной работе рассчитывались спектры одиночного непериодического видеоимпульса, периодической последовательности видеоимпульсов, одиночного непериодического радиоимпульса и периодической последовательности радиоимпульса.

Были рассмотрены методы вычисления спектра с помощью математического аппарата рядов Фурье, для одиночных непериодических импульсов, и свойства преобразования и интегралы Фурье, для периодических последовательностей импульсов.

Данная работа подтверждает, что спектр непериодического импульса дискретен, а спектр периодической последовательности сплошной.

Рассчитывая спектр радиоимпульсов был сделан вывод:

Спектральная плотность амплитуд модулированного сигнала занимает полосы частот вокруг и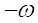. Она определяется смещением спектра огибающей сигнала по оси частот на величину вправо и влево. Поэтому определение спектра радиоимпульса свелось к нахождению спектра его огибающей.

Таким образом можно считать, что задачи курсового проекта достигнуты в полной мере.