Институт Кафедра
автоматизации и робототехники робототехники и мехатроники
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине
«Детали мехатронных модулей, роботов и их конструирование»
на тему
«Приводной модуль поворота звена робота»
Задание №16
Вариант №5
Выполнил
студент гр. АДБ-18-09: ______________ Маликов И.Т.
Принял
преподаватель: ______________ Буйнов М.А.
Москва 2020 г.
Практическое занятие № 2
Расчёт цилиндрической косозубой передачи
Провести расчёт цилиндрической косозубой реверсивной зубчатой передачи, если известны:
· максимальный вращающий момент на шестерне 1
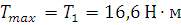
· передаточное отношение передачи U=2,5 ;
· циклограмма нагружения передачи
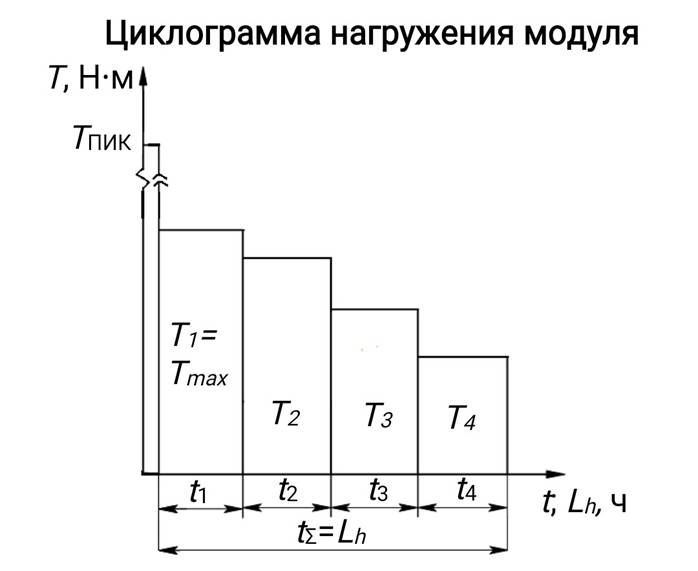
· значения моментов, углов поворота, время движения и коэффициент длительности работы передачи на i-ом участке нагружения соответственно:
 =16,6
Н∙м
=16,6
Н∙м
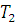 =15,8
Н∙м
=15,8
Н∙м
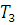 =14,1
Н∙м
=14,1
Н∙м
 =11,8
Н∙м
=11,8
Н∙м
 =1/2 рад
=1/2 рад
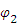 =4/7 рад
=4/7 рад
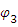 =7/9 рад
=7/9 рад
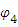 =4/5 рад
=4/5 рад
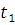 =0,6 c
=0,6 c
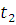 =0,6 c
=0,6 c
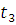 =0,9 c
=0,9 c
 =0,8 c
=0,8 c
 =0,43
=0,43
 =0,47
=0,47
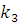 =0,06
=0,06
 =0,04
=0,04
 =
= ч
ч
Выбираем
материал шестерни 1 и колеса 2 Сталь 35ХМ объёмнозакленную с твёрдостью
HRC=55-50 и пределом текучести 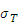 =330 MПа. Для дальнейших расчетов
принимаем HRC=53 МПа.
=330 MПа. Для дальнейших расчетов
принимаем HRC=53 МПа.
Допускаемые
контактные напряжения: [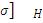 =
=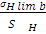 K
K
где предел контактной выносливости для шестерни и колеса:
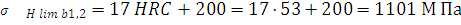 ;
;
 - коэффициент безопасности;
- коэффициент безопасности; 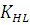 - коэффициент долговечности.
- коэффициент долговечности.
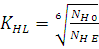 ,
,
где  - базовое число циклов изменения
контактных напряжений, для сталей
- базовое число циклов изменения
контактных напряжений, для сталей  -
-
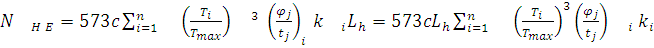 ,
,
где
с– число зацеплений в передачи (с=1);  вращающий мо-мент а i-ом участке
нагружения;
вращающий мо-мент а i-ом участке
нагружения;  максимальный вращающий момент;
максимальный вращающий момент;  и
и 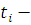 угол и время поворота шестерни на
i-ом участке нагружения;
угол и время поворота шестерни на
i-ом участке нагружения;  коэффициент длительности работы
пе-редачи на i-ом участке;
коэффициент длительности работы
пе-редачи на i-ом участке; 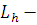 долговечность работы передачи.
долговечность работы передачи.
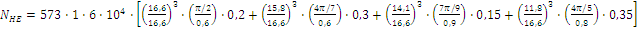 =66769121,8
ц
=66769121,8
ц
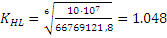
Допускаемые контактные напряжения:
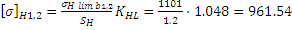 M Па;
M Па;
Предельное допускаемое изгибное напряжение
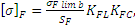
где предел изгибной выносливости для шестерни и колеса:
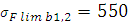 M Па.
M Па.
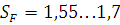 -коэффициент безопасности. Принимаем
-коэффициент безопасности. Принимаем .
.
 -коэффициент долговечности;
-коэффициент долговечности;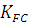 -коэффициент реверсивности. Принимаем
-коэффициент реверсивности. Принимаем
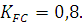

где  базовое число циклов изменения
изгибных напряжений, для сталей
базовое число циклов изменения
изгибных напряжений, для сталей
 ц ;
ц ;  эквивалентное число циклов изменения
изгибных напряжений:
эквивалентное число циклов изменения
изгибных напряжений:

 ц
ц
Так как эквивалентное число циклов, больше чем базовое число циклов изменения напряжений при изгибе
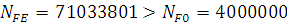 ,
,
то принимаем 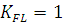 .
.
Допускаемые изгибные напряжения:
 М Па;
М Па;
Проектный расчёт передачи
Делительный диаметр шестерни
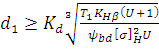 =
= мм
мм
Принимаем d1=26 мм.
В формуле КНβ – коэффициент неравномерности распределения нагрузки по ширине зубчатого венца. Его определяют по таблицам в зависимости от степени точности передачи и окружной скорости шестерни
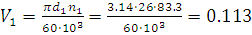 м/c.
м/c.
где 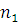 -частота вращения шестерни
-частота вращения шестерни
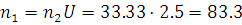 об/мин
об/мин
Выбираем степень точности передачи СТ=7. Тогда КНβ=1,05.
Делительный диаметр колеса
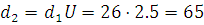 мм
мм
Межосевое расстояние
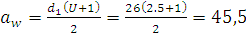 мм
мм
Модуль зубьев из условия контактной выносливости:
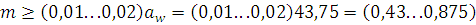 мм
мм
Модуль зубьев из условия изгибной выносливости:
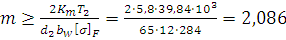 мм
мм
Здесь 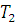 - вращающий момент на колесе 2
- вращающий момент на колесе 2
 мм
мм
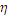 - коэффициент полезного действия
зубчатой передачи
- коэффициент полезного действия
зубчатой передачи
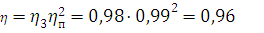 ;
;
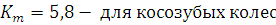


Принимаем  - коэффициент ширины зубчатого венца.
Принимаем
- коэффициент ширины зубчатого венца.
Принимаем 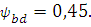 Окончательно выбираем модуль по
стандарту m=2,25 мм.
Окончательно выбираем модуль по
стандарту m=2,25 мм.
Для прямозубых колёс:
Вычисляем число зубьев шестерни
 .
.
Округляем полученное значение до целого числа и уточняем значение делительного диаметра

Находим число зубьев колеса
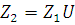
Округляем до целого значения и уточняем величину его делительного диаметра
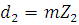 .
.
Вычисляем новое значение межосевого расстояния
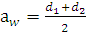 .
.
и действительное значение передаточного отношения

Определяем погрешность передаточного отношения и сравниваем с допускаемыми его значениями

Для косозубой передачи находим угол наклона зубьев.
Для этого вычисляем

При
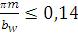 принимают
принимают 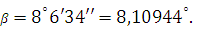
Так
как 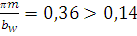 , то угол наклона зубьев будет равен
, то угол наклона зубьев будет равен

Угол
 не рекомендуют принимать больше
не рекомендуют принимать больше , поэтому увеличиваем ширину
зубчатого венца
, поэтому увеличиваем ширину
зубчатого венца 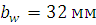 и находим новое значение угла
и находим новое значение угла 

Находим суммарное число зубьев шестерни и колеса
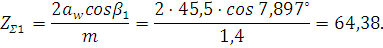
Округляем
 до меньшего целого
до меньшего целого 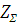 =64.
=64.
Окончательно угол наклона зубьев

Число зубьев шестерни
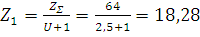 .
.
Округляем
 до целого ближайшего числа
до целого ближайшего числа
 =18.
=18.
При этом должно быть
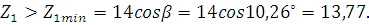
Принимаем
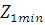 =14. Условие выполняется, так как
=14. Условие выполняется, так как
 =18 >
=18 >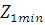 =14.
=14.
Для
прямозубых колёс  >
>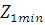 =14.
=14.
Вычисляем число зубьев колеса

Реальное передаточное отношение

Погрешность передаточного отношения
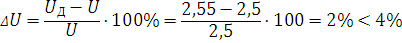
Коэффициент торцевого перекрытия

где
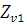 и
и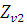 эквивалентное число зубьев:
эквивалентное число зубьев:
шестерни
 =
=
колеса
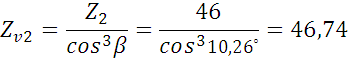
 =1,62>1,2 - условие выполняется
=1,62>1,2 - условие выполняется
Коэффициент осевого перекрытия

Если
условие не выполняется. Необходимо  увеличить, но неизвестно на сколько.
Поэтому bw увеличить можно в конце расчета передачи, когда будет известно
контактное напряжение
увеличить, но неизвестно на сколько.
Поэтому bw увеличить можно в конце расчета передачи, когда будет известно
контактное напряжение  .
.
Геометрические размеры зубчатых колёс
Начальные диаметры шестерни и колёса:
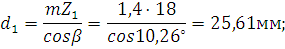
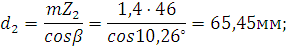
Диаметры окружностей вершин зубьев:
 мм
мм
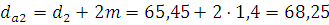 мм
мм
Диаметры окружностей впадин зубьев:

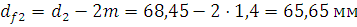
Проверочный расчёт зубьев на контактную выносливость
Условие контактной выносливости
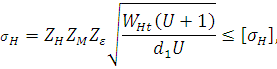
где  - коэффициент, учитывающий форму
сопряженных поверхностей зубьев
- коэффициент, учитывающий форму
сопряженных поверхностей зубьев

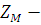 коэффициент, учитывающий механические
свойства материалов колёс
коэффициент, учитывающий механические
свойства материалов колёс

 коэффициент, учитывающий суммарную
длину контактных линий
коэффициент, учитывающий суммарную
длину контактных линий

 -коэффициент изменения длины
контактных линий.
-коэффициент изменения длины
контактных линий.
Для прямозубых колёс
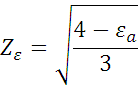
Удельная расчетная окружная сила

 – находим по таблицам для 7 степени
точности;
– находим по таблицам для 7 степени
точности;
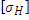 - допускаемое контактное напряжение.
- допускаемое контактное напряжение.
Вычисляем контактное напряжение

 =790 М Па
=790 М Па
Условие контактной выносливости выполняется.
В случае не выполнения условия контактной выносливости необ-ходимо ширину зубчатого венца увеличить
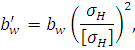
пересчитать
удельную расчетную окружную силу 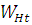 и снова найти контактное напряжение
и снова найти контактное напряжение 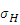 .
.
Ширина колеса

Ширина шестерни
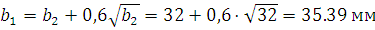
Принимаем
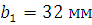
Проверочный расчёт зубьев на выносливость при изгибе
Условие изгибной выносливости

Эквивалентное число зубьев:
· шестерни

· колеса

По таблице выбираем значение коэффициентов форма зуба
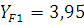 ;
; 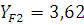 .
.
 коэффициент, учитывающий перекрытие
зубьев
коэффициент, учитывающий перекрытие
зубьев

 – коэффициент, учитывающий наклон
зубьев
– коэффициент, учитывающий наклон
зубьев

Вычисляем удельную расчетную окружную силу
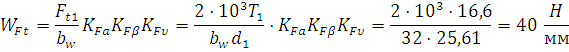
где
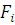 - окружная сила;
- окружная сила; 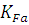 коэффициент неравномерности
распределения нагрузки между зубьями;
коэффициент неравномерности
распределения нагрузки между зубьями;

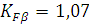 -коэффициент неравномерности
распределения нагрузки по длине зуба;
-коэффициент неравномерности
распределения нагрузки по длине зуба;
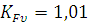 - коэффициент динамической нагрузки.
Коэффициенты
- коэффициент динамической нагрузки.
Коэффициенты  и
и 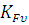 находим по таблице.
находим по таблице.
Вычисляем изгибные напряжения
· для шестерни
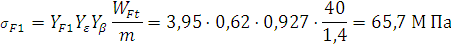
· для колеса
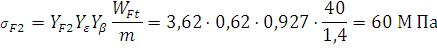
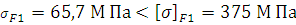

Условия выполняются
Силы в зацеплении
Силы на шестерне:
· окружная

· радиальная

· нормальная
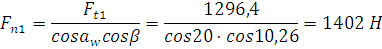
· осевая


Силы на колесе:
· окружная
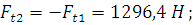
· радиальная

· осевая

· нормальная к зубу
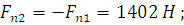
 .
.














 (zip - application/zip)
(zip - application/zip)










