|
47. Технические теории ползучести. Основные понятия Отметим, что в реальных условиях ползучесть, как правило, протекает при изменяющихся напряжениях и температурах, и для описания соответствующих процессов используются технические теории ползучести на базе характеристик, полученных при постоянных напряжениях и температуре. Обычно для оценки сопротивления материала ползучести получают серию кривых ползучести по результатам испытания образцов при различных постоянных уровнях напряжения. Обрабатывая эту серию кривых ползучести, можно определить константы и параметры аналитических зависимостей соответствующих теорий ползучести и определить пределы ползучести. Сущность теорий ползучести состоит в выборе основных переменных, определяющих процесс ползучести, и установлении функциональных зависимостей между ними. Известны четыре основные теории ползучести, построенные на различных гипотезах. Теория
течения. Основана на предположении существования постоянной
зависимости между скоростью пластической деформации, напряжением и
временем Теория
упрочнения. Под упрочнением
подразумеваются такие изменения в материале, которые происходят по мере
накопления деформаций ползучести и приводят к снижению скорости ползучести
при заданных напряжении и температуре. В данной теории предполагается
существование постоянной зависимости между пластической деформацией, скоростью
пластической деформации и напряжением Теории
наследственности и старения. В
этих теориях принята гипотеза о существовании постоянной зависимости между
пластической деформацией, напряжением и временем При линейной ползучести, если материал конструкции не обладает свойством старения, зависимость между напряжениями и деформацией можно представить в следующем виде:
где Для функции Для получения зависимости между напряжением и деформацией при линейной ползучести в теории наследственности взят принцип наложения, согласно которому суммарная деформация ползучести при переменном напряжении может быть найдена как сумма деформаций ползучести, вызванных соответствующими приращениями напряжений. При этом каждая величина деформации ползучести зависит только от величины этого приращения напряжения и продолжительности его действия, но не зависит от величины и длительности действия других приращений. Согласно принятому принципу наложения, получено выражение:
где t – время определения деформации; t0 –
момент времени приложения нагрузки; τ - момент времени
приращения нагрузки; функция Функция
где γ, k - постоянные коэффициенты, характеризующие свойства материалов. Первое слагаемое в выражении (18.7) соответствует упругой деформации, а интегральный член – деформации ползучести, накапливаемой в образце при действии нагрузки от момента времени t0 до t. Если учесть свойства старения материалов, то величина деформаций ползучести конструкций зависят от возраста материала. В этом случае физические уравнения можно представить в следующем виде:
где
Здесь β, n, A, B, γ - постоянные характеристики материалов конструкций. В общем случае, когда переменными являются как напряжение, так и деформация соотношения между ними с учетом свойства наследственности и строения в рамках линейной теории записывается в виде:
Здесь вводим обозначения:
Теория ползучести, в основу которой положено выражение (18.10), носит название теории наследственного старения. Соотношения наследственной теории ползучести были предложены Л.Больцманом в 1874 г. и развиты В. Вольтерра в 1909 г., а уравнения теории наследственного старения – Г.Н.Масловым и Н.Х.Арутюняном в 40-х годах XX столетия. Линейное соотношение между напряжениями и деформациями (18.10) отличается от закона Гука для упругого материала только тем, что вместо величины 1/E здесь имеется интегральный оператор. Отсюда следует следующее простое правило построения решения задачи теории линейной ползучести, которое носит название принцип Вольтерра. Решение задачи по теории линейной ползучести может быть получено из решения аналогичной задачи в упругой постановке, далее следует заменить упругие постоянные интегральные операторы и произвести необходимые операции над ними. В частности, если в известных упругих решениях предполагать, что они записаны в изображениях Лапласа, т.е. заменить упругие постоянные изображениями соответствующих операторов теории ползучести и применить операции переходов от изображений к оригиналам искомых функций, получим решение соответствующее задаче с учетом ползучести материалов конструкции. Отметим, что в настоящее время при решении многих инженерных задач, как в области механики твердого деформируемого тела, так и других отраслях, широко применяется метод интегрального преобразования Лапласа. Этот метод особенно эффективен при решении линейных дифференциальных, интегро-дифференциальных и интегральных уравнений, а также систем, состоящих из вышеуказанных типов уравнений. Суть его является следующей. Если имеется некая искомая функция y(t) от действительной переменной t, обозначая через y(s) образ искомой функции комплексной переменной s, т.е. изображение заданной функции по Лапласу, тогда формулы по определению оригинала и его изображения имеют следующие представления:
где i - мнимая единица, а c - некоторая постоянная, на действительной оси. В качестве примера реализации изложенного подхода при решении инженерных задач рассмотрим расчет прогиба свободного конца консольной балки (рис.18.6), в момент времени t = 0 загруженной равномерно распределенной нагрузкой, постоянной во времени. Материал балки характеризуется линейной ползучестью, для которого
Рис. 18.6 По методу начальных параметров в упругой постановке задачи решение записывается в виде:
Заменим
Тогда выражения перемещения (18.12) в изображениях Лапласа принимает вид:
Здесь K(s) определяется из (18.8):
С учетом (18.14), (18.13) принимает вид:
Выполняя операции обратного преобразования Лапласа, получим:
Отсюда следует, что при
действии постоянной нагрузки прогиб балки с течением времени возрастает по
экспоненциальному закону и при
где yA - упругое перемещение, т.е. перемещение балки в точке А при t = 0. В статически неопределимых упругих системах распределение усилий либо не зависит от упругих постоянных, либо зависит. В первом случае, как и в статически определимых системах, напряженное состояние при ползучести совпадает с напряженным состоянием упругой системы, если функции E(t), K(t,τ) одинаковы для всех элементов конструкции. Меняется только деформированное состояние. Во втором случае, который может встретиться, например, при расчете конструкций из разномодульных материалов, изменение во времени претерпевает не только деформированное, но и напряженное состояние. |
48 .Теория старения Согласно этой теории
предполагается, что при фиксированной температуре имеется определенная
зависимость между полной деформацией, напряжением и временем: Как указывалось выше, полная деформация складывается из мгновенной (упругой или упругопластической) деформации и деформации ползучести:
Существуют такие уровни напряжений и температур, при которых кривые ползучести оказываются подобными, т.с. их ход во времени оказывается одинаковым при различных напряжениях. В этом случае выражение для деформации ползучести, которая при фиксированной температуре является функцией напряжения и времени, можно записать в виде
В практических расчетах функцию Ч"(ст) часто считают степенной:
Тогда с учетом формул (4.1) и (4.3) уравнение ползучести теории старения записывается следующим образом:
где п > 1 — постоянная для данной температуры и материала величина. Числовое значение коэффициента п, вид и параметры функции Cl(t)устанавливают в результате обработки экспериментальных кривых ползучести, полученных в условиях одноосного напряженного состояния. Методика их определения иллюстрируется на примере кривых ползучести, показанных на рис. 4.5.
Рис. 4.5 Продифференцируем по времени функцию деформации ползучести (4.3), тогда с учетом того, что напряжение не зависит от времени, получим
Из рис. 4.5 очевидно, что в интервале времени от 40 до 100 ч в рассматриваемом диапазоне напряжений приближенно можно считать, что ползу- dO. п честь носит установившийся характер. Примем, что = В = const, и тогда ё„ = а"Б. Прологарифмировав это выражение, будем иметь
Запишем это равенство для напряжений ст = 20 МПа и а = 30 МПа. Учитывая, что при ст = 20 МПа
а при ст = 30 МПа ёп = 0,0007167 ч получим два уравнения
Решив эту систему уравнений, найдем «, = 4,477. Выполнив аналогичные вычисления для напряжений 20—25 и 25—30 МПа, найдем соответственно п2 = 4,475 и п3 = 4,48. Окончательно примем значение п = 4,48. Перейдем к определению функции Cl(t). Из формулы (4.3) следует, что
Примем ст = 20 МПа; по кривой ползучести, соответствующей этому напряжению, найдем деформации ползучести в различные моменты времени и но формуле (4.5) рассчитаем значения искомой функции. Найденные таким образом на основе экспериментальных данных (деформации ползучести) величины функции Q(() (МПа") приведены в табл. 4.1. Таблица 4.1
По найденным значениям построен график этой функции, показанный на рис. 4.6.
Рис. 4.6 Найдем аналитическое выражение этой функции. На участке неустано- вившейся ползучести (0—40 ч) аппроксимируем искомую функцию параболой четвертого порядка:
на участке установившейся ползучести (40—100 ч) аппроксимируем прямой:
Входящие в эти выражения
коэффициенты можно найти, используя значения Q, приведенные
в последней строке табл. 4.1, из следующих уравнений: В результате решения этой системы уравнений получим:
Таким образом, функция Q(/) опрелелена и деформации ползучести рассматриваемого материала при заданной температуре могут рассчитываться по формуле (4.3) с учетом соотношений (4.6), (4.7).
В рамках этого варианта теории старения рассмотрим процесс релаксации напряжений. Предположим, что стержень из стали 45Х14Н14В2М нагрет до температуры Т = 1093 К. Модуль упругости материала при этой температуре Е = = 3-101 МПа, предел текучести стт = 300 МПа. В начальный момент времени (t = 0) стержень мгновенно продеформи- ровали до деформации е0, и затем эта деформация поддерживается постоянной. В соответствии с формулой (4.4) в любой момент времени будет справедливо равенство
На рис. 4.7 показаны рассчитанные по этой формуле кривые релаксации напряжений при трех значениях мгновенных деформаций.
Рис. 4.7 Необходимо заметить, что теория старения имеет существенный недостаток: во все ее основные уравнения явно входит время, поэтому они не будут инвариантны относительно изменения начала отсчета времени. Как следствие этого, расчеты по этой теории в случае чередования нагрузки и разгрузки, при быстро меняющихся нагрузках могут привести к неверным результатам. Однако при плавно меняющихся во времени нагрузках расчеты по теории старения хорошо согласуются с результатами опытов. |
|||||||||||||||||||||||||||||||
|
49.Теория течения В теории течения предполагается, что при фиксированной температуре имеется определенная зависимость между скоростью деформации ползучести, напряжением и временем:
Если в рассматриваемом диапазоне напряжений и температур кривые ползучести подобны, то при степенной зависимости скорости деформации ползучести от напряжения уравнение этой теории записывается в виде
где п > 1 — постоянная для данной температуры п материала величина, a B(t) — положительная убывающая функция, которая при установившейся ползучести становится константой В{. Сопоставляя формулы (4.3) и (4.9), видим, что
Таким образом, в теории течения фигурируют также функция времени Q(?) и константа п, методика определения которых по экспериментальным кривым ползучести подробно рассмотрена выше. Считая, что полная деформация складывается из мгновенной упругой деформации и деформации ползучести, будем иметь
Продифференцировав это равенство по времени и учитывая формулу (4.9), получим основное уравнение теории течения
Рассмотрим в рамках этой теории процесс релаксации напряжения. Будем считать, что в момент времени t = 0 стержень продеформирован до величины е0 = о0/Е, которая в дальнейшем остается постоянной. Подставляя в левую часть уравнения (4.10) постоянное значение деформации е0, получим уравнение релаксации напряжения
Проинтегрировав это уравнение при начальном условии o(t = 0) = а0, получим
С увеличением времени напряжение убывает. Как очевидно, в основные уравнения теории течения также в явном виде входит время, поэтому она обладает теми же недостатками, что и рассмотренная выше теория старения. Пример 4.1. Определить напряжения в стержнях стержневой системы (рис. 4.8, а), все стержни которой одинаковы (I, = L2 = L., = 200 мм, Л, = Л2 = Л3 = = 1 мм2), изготовлены из стали 45Х14Н14В2М и нагреты до температуры 1093 К. В момент времени t = 0 к узлу А приложена сила F= 45 Н, и далее она остается постоянной. Модуль упругости и предел текучести этой стали при указанной температуре равны Е = 3-101 МПа, ат = 300 МПа.
Рис. 4.8 Решение. Осуществляя процедуру метода сечений (рис. 4.8, б), запишем уравнения равновесия узла А:
Из этих уравнений следует, что
Разделив эти равенства на площади поперечных сечений стержней (Л), найдем
Как очевидно, задача является статически неопределимой, поэтому рассмотрим дополнительно геометрическое соотношение, связывающее деформации среднего и какого-либо крайнего стержня. Из рис. 4.8, в следует, что ДL3 = ДА,cos а, или
Заметим, что полученные соотношения (4.12) и (4.13) справедливы при любом времени, так как они являются следствием только уравнений равновесия и геометрических соотношений. Продифференцировав соотношение (4.13) по времени, получим
Найдем с помощью формулы (4.10) скорости деформаций первого и второго стержней:
Учитывая, что в силу соотношений (4.12) сг3 = F/A - а,, а а;, = -а,, скорость деформации третьего стержня выразим через напряжение в первом стержне и скорость его изменения:
Таким образом, равенство (4.14) с учетом соотношений (4.15) и (4.16) можно записать в виде Отсюда
Проанализируем напряженное состояние стержневой системы. В начальный момент времени (f = 0) в соответствии с формулой (4.12) сумма напряжений равна а3 + а, = F/A = 30/1 = 30 < ат, и, следовательно, начальные напряжения являются упругими. Таким образом, в силу формул (4.12) и (4.13) будем иметь Отсюда
При установившейся
ползучести скорость деформации и функция B(t) должны быть
постоянными (?, = const, B(t) = В, = const), поэтому из
формулы (4.18) получим Так как в любой момент
времени в силу формулы (4.12) ст3 + а, = F/A, то При п = 4,477 найденные напряжения будут равны
Из приведенных данных ясно, что на участке нсустановившсйся ползучести напряжение в центральном стержне падает, а в крайних стержнях возрастает. На этом участке напряжение в первом стержне находят из уравнении (4.18), которое можно преобразовать к виду
Вычисления по этой формуле могут производиться следующим образом: задавшись каким-либо напряжением из диапазона ст0| — а|уст (например, а = 26 МПа) вычисляют интеграл (/ = 1,882 10 6 МПа"), далее находят момент времени, при котором правая часть равенства (4.20) окажется равной интегралу. Так устанавливается связь между временем и соответствующим ему напряжением. Расчеты приводят к результатам, указанным в табл. 4.2. Таблица 4.2
По этим данным построен график о,(7), приведенный на рис. 4.9.
Рис. 4.9 Для дальнейших вычислений удобно аппроксимировать эту кривую параболой четвертого порядка. Таким образом: · • при t = 0 <т01 = 0.667F//1 = 30 МПа; · • при 0 <<="" i="">1 ч ст, (0 = 30 - 47,632f + 189.648Г2 - 406,94+ 361,874гф · • при t > 1 ч ст1уст = 24,238 МПа. Установив напряжение в первом стержне, можно с помощью формулы (4.12) найти напряжения в остальных стержнях стержневой системы. Определим перемещение узла А. Из формулы (4.15) следует, что
График перемещения узла приведен на рис. 4.10.
Рис. 4.10 |
50.Теория упрочнения В теории упрочнения
предполагается, что при фиксированной температуре существует зависимость
между деформацией ползучести, ее скоростью и напряжением: Заметим, что, в отличие от первых двух теорий, в основном уравнении этой теории время в явном виде не содержится.
Наиболее распространенным является степенной вариант теории упрочнения, согласно которому основное уравнение этой теории записывается в виде где a, b, С — функции только температуры, определяемые по кривым ползучести. Из этой формулы очевидно, что при постоянном напряжении по мере увеличения деформации ползучести ее скорость уменьшается, материал становится как бы более прочным (менее податливым), отсюда и название теории — теория упрочнения. Найдем выражение деформации ползучести как функции напряжения и времени. Для этого соотношение (4.22) перепишем следующим образом:
Рассмотрим случай, когда напряжение и температура постоянны во времени. Тогда, интегрируя это уравнение при условии, что еи(? = 0) = 0, получим выражение для деформации ползучести
Рассмотрим теперь условия применимости степенного варианта теории упрочнения и методику определения материальных констант а, b и С на примере стали 40Х14Н14В2М, кривые ползучести которой при температуре 1093 К приведены на рис. 4.5. Прологарифмируем выражение (4.24), тогда
Из этого выражения ясно, что при заданной температуре в координатах «lgеп— lgt» при фиксированных значениях напряжений и в координатах «lge„ — lga» при фиксированных значениях времени должны получаться параллельные прямые, если в рассматриваемых режимах нагружения а, b и С в действительности являются константами материала. Па рис. 4.11 и 4.12 точками показаны значения lgeM, найденные по экспериментальным кривым ползучести (см. рис. 4.5), а сплошными параллельными прямыми — их возможная аппроксимация. Ясно, что с достаточно большой степенью точности она возможна, что свидетельствует о правомерности применения степенного варианта теории упрочнения. С помощью этих рисунков находим tga и tg (3. Из формулы (4.25) следует, что tga = 1/(1 + а) и tgP = b/{ 1 + а). Таким образом, получаем следующие значения первых двух констант:
Рис. 4.11 Рис. 4.12 Определим теперь числовое значение константы С. Из
формулы (4.25) находим Зная а и Ь, по этой формуле вычисляют значения lgС, а затем и С при напряжениях 20, 25, 30 МПа и времени 10, 20, 30, 40, 100 ч. Полученные 15 значений осредняют и находят С = 10 1766 МПа 8829-ч Таким образом, деформации ползучести стали 40Х14Н14В2М при температуре 1093 К в рассматриваемом диапазоне изменения напряжений и времени вычисляются по формуле
На рис. 4.13 кружками показаны экспериментально найденные деформации ползучести рассматриваемой стали, а сплошными линиями — рассчитанные по приведенной формуле кривые ползучести. Как очевидно, совпадение вполне удовлетворительное.
Рис. 4.13 На рис. 4.14 показаны кривые ползучести, рассчитанные но формуле (4.24) при постоянном и стуненчато-неременном напряжениях.
Рис. 4.14 Теперь рассмотрим в рамках этой теории процесс релаксации напряжения. Допустим, что в момент времени t = 0 стержень мгновенно продефор- мирован и деформация г = ст(/ = О)//; зафиксирована. В последующие моменты времени напряжение будет уменьшаться. Выведем эту зависимость напряжения от времени.
По определению полная деформация в произвольный момент времени равна Мгновенная деформация определяется величиной действующего в данный момент времени напряжения, поэтому в силу формулы (4.27) будем иметь о(0)/Е = а/Е + еп(ст, t), или
Подставим это выражение в формулу (4.23), тогда
Проинтегрировав это равенство с учетом того, что при t = 0 о = а(0), получим
Предположим, что стержень из стали 45Х14Н14В2М нагрет до температуры Т= 1093 К. Модуль упругости материала при этой температуре Е = = 3-104 МПа, предел текучести стт = 300 МПа. Пусть в начальный момент времени (t = 0) стержень мгновенно проде- формировали до деформации ?0 = 10 3 и затем эта деформация поддерживается постоянной. Этой деформации соответствует напряжение а(0) = ?е0 = = 30 МПа. При а = а(0) интеграл обращается в нуль и в силу равенства (4.28) время также должно быть равно нулю. Зададимся напряжением а = 28 МПа и вычислим интеграл, поделив который на СЕ"*а, найдем время, соответствующее принятому значению напряжения. Поступая аналогичным образом, установим зависимость между напряжением и временем, определяющую процесс релаксации напряжения при фиксированной деформации е0 = 10 3. На рис. 4.15 приведена эта кривая релаксации.
Рис. 4.15 Пример 4.2. Балка, показанная на рис. 4.16, изготовлена из стали 45Х14Н14В2М и нагрета до температуры Т = 1093 К. Определить величину ее максимального прогиба к 80-му часу после нагружения, если d = 10 мм, h = 20 мм, L = 200 мм, М = 10 000 Н ? мм. В расчетах принять Е = 3 • 10" МПа, о, = 300 МПа.
Рис. 4.16 Решение. В
момент нагружения (t = 0) максимальное нормальное напряжение
в балке будет равно сттал.= M/W = 14,9 МПа. Оно
меньше предела текучести материала при заданной температуре, и поэтому is
начальный момент времени балка деформируется упруго, нормальные напряжения
линейно меняются но высоте поперечного сечении, а максимальный прогиб
рассчитывается по формуле
Рис. 4.17 В произвольный момент времени (t > 0) прогиб будет складываться из начального значения и прогиба, обусловленного ползучестью материала (рис. 4.17): Считая справедливой гипотезу плоских сечений, запишем выражение для деформации ползучести произвольного слоя балки в виде
где z — расстояние рассматриваемого слоя от нейтрального: kn — изменение кривизны балки за счет деформации ползучести. Подставляя выражение (4.30) в исходное соотношение теории упрочнения (4.22), получим следующее выражение для нормального напряжения:
С учетом этого уравнения равновесия части балки, расположенной левее сечения с координатой «х» (см. рис. 4.17), запишутся в виде
h/2 где J = d | z(-l*a+b)dz — приведенный момент инерции поперечного сечения -h/2 относительно нейтральной оси, которая в прямоугольном поперечном сечении проходит через его центр тяжести и совпадает с осью у. Из формулы (4.32) следует, что
Интегрируя это уравнение при условии kn(t =0) = 0, получим
Будем предполагать, что прогибы малы, тогда k = —f и, учитывая формулу (4.33), будем иметь
В рассматриваемом случае чистого изгиба правая часть этого уравнения является функцией только времени. Интегрируя его дважды по х при граничных условиях va(x = 0) = vn(x = L) = 0, получим выражение для vtt(x, t). В частности, его максимальное значение в произвольный момент времени равно
На рис. 4.18 показан рост во времени полного прогиба в среднем сечении балки. Таким образом, к 80-му часу после нагружения балки прогиб в среднем сечении составляет 1,52 мм. На рис. 4.19 приведены эпюры нормальных напряжений по поперечному сечению балки в момент нагружения а(/ = 0) и в произвольный момент времени 0). Анализируя эти эпюры, заключаем, что в процессе ползучести нормальные напряжения перераспределились, их зависимость от координаты стала нелинейной, а максимальное значение оказалось меньше, чем в момент нагружения.
Рис. 4.18 Рис. 4.19 |
|||||||||||||||||||||||||||||||
|
51.Теория ползучести с анизотропным упрочнением Теориях ползучести предполагалось, что упрочнение является изотропным. Экспериментальные исследования ползучести при сложном нагружении указывают на существенно анизотропный характер упрочнения в условиях ползучести. Учет деформационной анизотропии может быть произведен так же, как это сделано в теории пластичности, путем разделения тензора напряжений на тензоры активных и добавочных напряжений [501. На возможность построения такой теории было указано Генки 1221 и Д. Д. Ивлевым [31]. Ниже изложена теория ползучести с анизотропным упрочнением, разработанная Г. М. Хажинским [48, 103, 126]. Примем, что тензор напряжения atj может быть представлен в виде суммы двух тензоров: активного а,-у и добавочного х*/ напряжений о,-у = а,у -f- Xij? Допустим, что девиаторы полных s,y, активных р,у и добавочных pi;- напряжений могут быть представлены в аналогичном виде s,y = (5,у -)- р?у и что для одноосного напряженного состояния два главных напряжения тензоров активных и добавочных напряжений равны нулю. Примем, что течение имеет потенциал, поверхность которого в пространстве компонентов девиатора напряжений является гиперсферой, центр которой задается девиатором добавочного напряжения. Выражение для потенциала имеет вид /, = = ЗР,уР,//2. Согласно определению потенциала скоростей деформаций ползучести компоненты скоростей деформаций ползучести даны формулой (3.16). Потенциал не зависит от среднего нормального напряжения. Направление вектора скорости деформации, которое согласно формуле (3.16) нормально к поверхности потенциала, не изменяется при смещении ее как жесткого целого. Поэтому
Подставим эту величину в
выражение для интенсивности скоростей деформаций ползучести (3.17). Тогда,
используя соотношение (3.8), получим I = Й/(2а,) и,
следовательно, Примем, что интенсивность скоростей деформаций ползучести является произведением двух функций:
одна из которых G — G (Ф) — функция температуры, а вторая Q = Q (а,) — функция интенсивности активного напряжения. Функция G обычно принимается в форме, которая
была рассмотрена в где Gx — постоянная для материала; Atff — энергия активации ползучести; R— газовая постоянная; Т — абсолютная температура. Функция интенсивности
активного напряжения может быть принята в одной из форм, о которых говорилось
ранее (§ 2 и 8): степенная зависимость
закон гиперболического синуса экспоненциальная зависимость Использование экспоненциальной зависимости позволяет значительно упростить расчеты, однако она несправедлива при малых напряжениях, так как Q (0) Ф 0. Допустим, что приращение
компонентов девиатора добавочного напряжения зависит от компонентов
приращения деформации ползучести, а также приращения времени и может быть
представлена в форме где А и D —
функции температуры, которые могут быть представлены в форме (3.31): АНГ — энергия активации возврата; Q (х,) — функция интенсивности добавочных напряжений, такая же, как Q (а,). Для уточнения теории, особенно при напряжениях выше предела пропорциональности, можно принять, что величина А является функцией не только температуры, но также и интенсивности напряжения о,- [481. При записи соотношения (3.35) использована идея Бейли [111 1 о том, что в процессе ползучести механическое упрочнение (первое слагаемое) взаимодействует с термическим разупрочнением (второе слагаемое с отрицательным знаком).
Перейдем к частному случаю одноосного напряженного состояния, при котором |f = ||с|; О/ =- |а | = |а 4-х|; а* = = |а|; Xi = IXI* Р = 2//3. Вначале используем степенную зависимость (3.32). Тогда из соотношений (3.30), (3.32) и (3.35) получим где символами sign (а — х)» sign % обозначены знаки величин о—х и х соответственно. Рассмотрим вначале ползучесть при постоянном напряжении. Если до начального момента времени ползучесть отсутствовала и напряжение было меньше, чем предел пропорциональности материала при температуре испытания, то добавочное напряжение в начальный момент времени равно нулю и активное напряжение равно приложенному. В дальнейшем происходит увеличение во времени добавочного и уменьшение активного напряжений. Получим уравнение кривых ползучести при постоянном напряжении. Учитывая, что в рассматриваемом случае sign (а — — х) = +1. sign х = +1, из соотношений (3.36) и (3.37) получим
и, следовательно,
Используя выражение (3.36),находим, что Принимая во внимание соотношение (3.38), получаем
Введем безразмерную величину и = Г/о.
Следовательно, Для случая ползучести при постоянном напряжении dx = о
йу и уравнения (3.38) и (3.39) преобразуются к виду где а = D/(AG). Из формулы (3.36) имеем Iе = G (а/сДл (1 — у)п. Так как скорость деформации ползучести при определенном значении
времени tn разграничивающем первую и вторую
стадии ползучести, и соответствующем ему значении уг, становится
ПОСТОЯННОЙ И минимальной (Imin). ТО Поскольку в начальный момент времени t = 0 добавочное напряжение % — 0 и, следовательно, у = 0, а затем с течением времени добавочное напряжение %и величина у растут, значение уг представляет собой наибольшую величину у.Она не зависит от времени. Если принять, что минимальная скорость деформации ползучести является степенной функцией напряжения, то из формулы (3.43) следует, что ут не зависит от напряжения, и так как температура отражается коэффициентом G, то величина уг является постоянной для материала. Интегрируя уравнения (3.41) и (3.42) и используя начальные условия t = О, X =0. У — 0, ес = 0, получаем
где очевидно, что
Уравнения (3.43) и (3.45) позволяют определить величины п, G, уг и а.Уравнения (3.44) являются уравнениями кривой ползучести в параметрической форме (параметром является величина у). Получим теперь уравнение кривой релаксации напряжений при постоянной деформации. Используя уравнение (2) и учитывая, что в рассматриваемом случае sign (а — х) = +1 и sign х — 1, преобразуем уравнения (3.36) и (3.37) к виду
Интегрируем это уравнение, используя начальное условие: при I — О У = 0:
Уравнения (3.55) и (3.58) являются уравнениями кривой релаксации при постоянной деформации в анзотермической форме (параметром по-прежнему является величина у). Рассмотрим теперь ползучесть при ступенчатом нагружении. Как и раньше, представим себе, что вначале образец испытывается на ползучесть в течение времени при напряжении σ1,а затем напряжение мгновенно увеличивается до величины σ2. Очевидно, что как при напряжении σ1так и при напряжении σ2 ползучесть описывается уравнениями (3.44), по которым можно построить кривые ползучести при постоянных величинах этих напряжений. После изменения напряжения с σ1 до σ2 ползучесть описывается кривой при напряжении σ2, взятой от точки, абсцисса которой t2 определяется величиной добавочного напряжения X1, возникшего в результате ползучести при напряжении σ1. Согласно первой формуле (3.44) t2 = t, (σ1/ σ2)n-1 Ф2/Ф1, причем = Ф1=Ф1 (у1,а); Ф2 =(у2, а); у1 = X1/ σ1; у2= X1/ σ2 Выведем теперь уравнение кривой обратной ползучести. В этом случае может быть рассмотрен процесс ступенчатого нагружения при мгновенном уменьшении напряжения от σ до 0. Тогда sign (σ —х) =—1, sign х = +1 и уравнения (3.36) и (3.37) принимают вид
Проинтегрируем уравнение (3.60), учитывая, что при t = t1 (рис. 3.1) Х = X1- Получим
Добавочное напряжение, возникшее в результате ползучести при напряжении а, в течение времени tv определяется при помощи первого уравнения (3.44) и соотношения (3.40). Подставим выражение (3.61) в уравнение (3.59). Используя
соотношение (1.1), получим Интегрируя это уравнение и используя начальное условие при t = tu tc = ef (см. рис. 3.1), получаем
Эта формула позволяет определить уменьшение деформации ползучести е, = е" — ес после разгрузки. Используем теперь закон гиперболического синуса (3.33) Из соотношений (3.30), (3.33) и (3.35) для частного случая одноосного напряженного состояния имеем
Получим вначале из этих
выражений уравнение кривых ползучести при постоянном напряжении, учитывая,
что в этом случае sign (а —х) — +1* s>gn X
= +1- Из соотношений (3.63) и (3.64) имеем и, следовательно,
Проинтегрируем это выражение, используя начальное условие: при t = 0 х =0. В результате преобразований получим
где для получения уравнения кривой ползучести подставим выражение (3.65) в уравнение (3.63), учитывая, что sign (о — х) = = 1, и соотношение (1.1):
Проинтегрируем это выражение, принимая во внимание, что при t — 0 гс = 0. После преобразований находим уравнение кривой ползучести при постоянном напряжении
Получим теперь уравнение кривой релаксации при постоянной деформации. Используя уравнение (2) и учитывая, что в рассматриваемом случае sign (а — х) = +1 и sign % = +1, преобразуем уравнения (3.63) и (3.64) к виду
Поделив второе уравнение на первое, получаем Это дифференциальное
уравнение может быть проинтегрировано только численно. При этом необходимо
использовать начальное условие: при / = 0, ц = 0 о=а (0). В результате
численного интегрирования устанавливаем функцию х — X (°)- После
этого может быть проинтегрировано уравнение (3.67). В результате получаем
уравнение кривой релаксации при постоянной деформации Ступенчатое нагружение и обратная ползучесть могут быть рассмотрены так же, как и в случае использования степенной зависимости. Рассмотрим экспериментальную проверку теории ползучести с анизотропным упрочнением. Результаты экспериментального исследования ползучести при ступенчатом нагружении (рис. 3.2, 3.3) показывают, что они лучше согласуются с данными, полученными по теории ползучести с анизотропным упрочнением, чем по теории упрочнения. На рис. 3.2 представлены результаты испытания двух образцов, описанные в работе 120]. Один из образцов (а) в течение 10 ч деформировался при напряжении а — 400 МПа, а затем в течение 40 ч при напряжении а = 300 МПа, а другой образец (b) Рис. 3.3. Экспериментальная (сплошная линия) и теоретические кривые ползучести при ступенчатом нагружении для образцов из алюминиевого сплава при температуре 150° С: штриховая линия — по теории ползучести с анизотропным упрочнением, штрихпунктирная — по теории упрочнения [1261
Рис. 3.2. Экспериментальная (сплошная линия) и теоретические кривые ползучести при ступенчатом нагружении для образцов жаропрочного сплава на никелевой основе при температуре 700° С: штриховая линия — по теории ползучести с анизотропным упрочнением, штрих- пунктирная — по теории упрочнения [20 j испытывался в обратном порядке: вначале в течение 40 ч при напряжении а = 300 МПа, а затем в течение 10 ч при напряжении а = 400 МПа. Как следует из кривых ползучести, деформация второго образца сказывается несколько больше, чем первого. Это описывается теорией ползучести с анизотропным упрочнением, а теория упрочнения дает качественно обратный результат. На рис. 3.3 представлены результаты испытаний, проведенных В. С. Наместниковым 163). Интересно отметить, что при напряжениях выше предела пропорциональности (рис. 3.3, а) теория упрочнения приводит к завышенным деформациям после догрузки по сравнению с экспериментом, а при напряжениях ниже предела пропорциональности (рис. 3.3, б) — наоборот. Как указывалось выше, при ступенчатом нагружении в случае увеличения напряжения теория течения дает кривую ползучести, расположенную ниже кривой по теории упрочнения, т. е. еще хуже согласуется с опытом, чем теория упрочнения, а теория старения вообще не отражает ступенчатого нагружения. Поэтому сопоставление экспериментальных данных с результатами, полученными по теориям течения и старения, не производилось.
Рис. 3.4. Экспериментальные (сплошные линии) и теоретические (штриховые линии) кривые обратной ползучести для жаропрочного сплава на никелевой основе при температуре 700° С (20J Результаты экспериментального исследования обратной ползучести (рис. 3.4 и рис. 3.5) показывают, что они хорошо согласуются с данными, полученными по теории ползучести с анизотропным упрочнением. На рис. 3.4 представлены результаты опытов, описанных в работе [20), а на рис. 3.5 — данные обширного экспериментального исследования, проведенного Джонсоном [122]. Очень интересны результаты экспериментального исследования ползучести при неодноосном напряженном состоянии в случае изменяющихся во времени нагрузок. При таких испытаниях проверяется не только гипотеза о существовании потенциала ползучести, но также и теория ползучести.
Рис. 3.6. Экспериментальная (сплошная линия) и теоретические кривые ползучести при знакопеременном прямом (/) и обратном (2) кручении образцов из алюминиевого сплава при температуре 150°С и напряжении т* 140 МПа: штриховая линия — по теории ползучести с анизотропным упрочнением, штрихпунктирная — по теории упрочнения [126]
Рис. 3.5. Экспериментальные (сплошные линии) и теоретические (штриховые линии) кривые обратной ползучести для малоуглеродистой стали при температуре 455ЭС после предварительной ползучести [126] Рис. 3.7. Экспериментальная (сплошная линия) и теоретические кривые ползучести трубчатых образцов из малоуглеродистой стали при температуре 450° С: штриховые линии — по теории ползучести с анизотропным упрочнением, штрихпунктирные — по теории упрочнения [126] На рис. 3.6 сопоставлены теоретические данные с результатами испытаний на ползучесть трубчатых образцов, проведенных В. С. Наместниковым 161 ] по следующей программе. Вначале образец деформировался в течение 50 ч при постоянном во времени крутящем моменте, создающем постоянное касательное напряжение, затем разгружался и вновь нагружался таким же по величине, но обратным по направлению постоянным во времени крутящим моментом и вновь испытывался в течение 50 ч. Абсолютная величина деформации сдвига при обратном кручении больше, чем при прямом. Следовательно, предварительное кручение, по знаку обратное последующему, раз- упрочняет материал при последующем кручении. На рис. 3.7 сопоставлены результаты экспериментального исследования ползучести при сложном нагружении, проведенном Джонсоном (124], и теоретические данные. Вначале тонкостенные трубки из углеродистой стали растягивались в течение 25 ч (а = 112 МПа), а затем в течение такого же времени растягивались и скручивались (а = 112 МПа, а = 18,6 МПа). Из графиков следует, что теория ползучести с анизотропным упрочнением значительно лучше описывает ползучесть при сложном нагружении, чем теория упрочнения. |
52. Экспериментальная проверка и анализ теорий ползучести Наиболее простым способом экспериментальной проверки различных теорий ползучести является сопоставление экспериментальной кривой релаксации при постоянной деформации с теоретическими кривыми, построенными по различным теориям ползучести.На рис. 2.9—2.11 сопоставлены теоретические кривые релаксации напряжений с экспериментальными, полученными в опытах Дэвиса [117] (рис. 2.9), Джонсона [123] (рис. 2.10), а также в опытах Ю. Н. Работнова, В. И. Даниловский и Г. М. Ивановой [26] (рис. 2.11). Как следует из рис. 2.9 и 2.10, экспериментальная кривая релаксации располагается между теоретическими кривыми по теориям старения и течения. Теория упрочнения хорошо подтверждается экспериментально (см. рис. 2.11).Рис. 2.9. Экспериментальная (сплошная линия) и теоретические кривые релаксации для меди при температуре 165° С и начальном напряжении о (0) = = 94,9 МПа: штриховая линия — по теории старения в формулировке (2.3), штрихпунктир- ная — по теории течения в формулировке (2.4)
Рис. 2.10. Экспериментальная (сплошная линия) и теоретические кривые релаксации для хромомолибденовой стали при температуре 525° С и начальном напряжении о (0) = 146 МПа: штриховая линия — по теории старения в формулировке (2.3), штрихпунктир- ная — по теории течения (2.4)Рассмотрим результаты экспериментального исследования релаксации при постоянной деформации после предварительной ползучести при постоянной растягивающей силе и после предварительного растяжения за пределы упругости, описанного в работе 126]. В первой группе опытов образцы вначале испытывались на ползучесть в течение 25 ч при напряжении а = 200 МГ1а, а затем в течение 50 ч в условиях релаксации при начальном напряжении о (0) = 200 МПа. Во второй группе опытов образцы растягивались с постоянной скоростью нагружения до тех пор, пока пластическая деформация не достигала такой же величины, как и в первой группе опытов, при испытаниях на ползучесть. Соответствующее напряжение было, очевидно, больше, чем в первой группе опытов. После этого напряжения быстро снижались до величины а (0), и затем проводились испытания в условиях релаксации. Такие испытания ставились для того, чтобы сопоставить влияние на релаксацию наклепа, вызванного кратковременным растяжением и ползучестью. Как следует из рис. 2.12, предварительная ползучесть сильно замедляет релаксацию, а кратковременный наклеп почти не скачет.
Рис. 2.11. Экспериментальные кривые (сплошные линии) релаксации для хромо- молибденовой стали 30ХМ при температуре 500° С и различных начальных напряжениях и теоретические кривые (штриховые линии), построенные по теории упрочнения в формулировке (2.7) и (2.8) зывается на релаксации. Это говорит о различиях протекания процессов ползучести и кратковременной пластической деформации. Из сопоставления экспериментальных / и 3 и теоретических 2 и 4 кривых релаксации также следует, что теория упрочнения хорошо подтверждается экспериментально. Рассмотрим экспериментальную проверку различных теорий ползучести при ступенчатом нагружении. На рис. 2.13—2.15 представлены результаты экспериментального изучения ползучести при ступенчатом нагружении металлических образцов и проведено сопоставление их с теоретическими данными по теориям упрочнения и теориям нелинейной наследственности. На рис. 2.16—2.17 приведены данные опытного изучения ползучести при ступенчатом нагружении полимерных образцов по программам, изображенным на рис. 2.18. Сплошной линией представлены кривые ползучести при постоянных напряжениях, равных напряжениям, действующим на каждом этапе ступенчатого процесса; кружки и точки — результаты испытаний при ступенчатом нагружении, штриховые линии — теоретические кривые по теории нелинейной наследственности с использованием принципа сложения деформаций. В опыте по программе а напряжение принимало последовательно значения 15 и 10 МПа, по программе б — 10 МПа и 0. В опытах по программе Ь напряжение принимало периодические значения 14, 16, 14 и 0 МПа, по программе г— 14, 20, 26 и 20 МПа [151. На рис. 2.19 и 2.20 приведены результаты опытного изучения " релаксации при ступенчатом деформировании полимерных образцов по программам, изображенным на рис. 2.21. Сплошными линиями представлены кривые релаксации при постоянных деформациях, равных деформациям на каждом этапе ступенчатого процесса; точки, кружки и квадратики отражают результаты испытаний при ступенчатом деформировании, штриховые линии — теоретические кривые по теории нелинейной наследственности с использованием принципа сложения напряжений. В опыте по программе а нижний уровень деформации был равен 0,8%, верхний-— 1,2%, в опытах по программе б—верхний и нижний уровни деформации были равны 1,2 и 0,4% (кружки) и 1,2 и 0,8% (точки). В опытах по программам Ь иг деформация принимала периодически значения 0,8 и 1,2% [15]. Таким образом, из рассмотренных выше теорий ползучести для полимеров хорошо согласуется с данными опыта нелинейная теория наследственности, а для металлов — теория упрочнения и нелинейная теория наследственности. Теория упрочнения лучше согласуется с экспериментальным исследованием релаксации при постоянной деформации, чем теория пластической наследственности. Последняя в отличие от
Рис. 2.13. Кривые ползучести при постоянных и ступенчатых нагрузках для образцов из красной меди при температуре 200° С по теории пластической наследственности (сплошные линии) и теории упрочнения (штриховые линии): О — результаты опытов при постоянной нагрузке, X — при ступенчатой 75 МПа в течение 15 ч и затем 105 МПа [29] Рис. 2.12. Экспериментальные (сплошные линии) и теоретические (штриховые линии) кривые релаксации для хромомолибденовой стали 30ХМ при температуре 500° С и начальном напряжении о (0) — 200 МПа после предварительной ползучести (/ и2) и после кратковременного наклепа (3 и 4). 5 — кривая релаксации без наклепа (26 J
Рис. 2.14. Кривые ползучести при ступенчато-изменяющем- ся напряжении 80—160 МПа. Материал — дюралюминий. Температура испытания 200° С: штриховая линия — по теории упрочнения в формулировке (2.7) и (2.10), сплошная — но несколько видоизмененной теории упрочнения [59]; Л, о. • — результаты испытаний трех образцов [59]
Рис. 2.15. Кривые ползучести при ступенчато-изменяющсмся напряжении, увеличивающемся от 80 до 160 МПа и уменьшающемся от 160 до 80 МПа. Материал—дюралюминий. Температура испытания 200° С: сплошные линии — но теории пластической наследственности Ю. Н. Работнова, штриховые — по теории нелинейной наследственности Н. X. Арутюняна и М. И. Розовского [60]
Рис. 2.18. Программы испытаний, результаты которых приведены на рис. 2.16 и 2.17 Рис. 2.19. Кривые релаксации при постоянном и ступенчатых деформированиях для образцов из целлулоида (программы а и б)(15)
Рис. 2.21. Программы испытаний, результаты которых приведены на рис. 2.19 и 2.20 Рис. 2.20. Кривые релаксации при постоянном и ступенчатом деформированиях для образцов из целлулоида (программы в и г) [15]
Рис. 2.16. Кривые ползучести при постоянной и ступенчатых нагрузках для образцов из полиэфирной смолы (программы а и б) [15]
Рис. 2.17. Кривые ползучести при постоянной и ступенчатых нагрузках для плоских образцов из плекснглаза (программы в и г) [15] теории упрочнения отражает явление обратной ползучести, однако, как будет показано в следующей главе, дает сильно завышенные величины деформаций обратной ползучести. Невозможность отражения явления обратной ползучести теориями упрочнения, течения и старения объясняется тем, что в основные уравнения этих теорий в отличие от уравнений наследственных теорий не входят интегральные операторы. Теория старения предполагает наличие функциональной связи между деформацией, напряжением и временем. В действительности это невозможно, так как наличие такой связи означало бы, что величина деформации е в момент времени t не зависит от процесса нагружения, т. е. от напряжений в моменты времени, предшествующие моменту /, что противоречит опыту. Недостатком теории течения (так же, как и теории старения) является то, что в основное уравнение ее время включено явным образом, вследствие чего это уравнение неинвариантно относительно изменения начала отсчета времени. Однако при плавно изменяющихся нагрузках теории старения и течения хорошо согласуются с результатами опытов. |
|||||||||||||||||||||||||||||||
|
53. Особенности кратковременной ползучести Кратковременная ползучесть ( в течение 6 ч) большинства типов тензорезисторов, погруженных в трансформаторное масло при атмосферном давлении, не отличается от кратковременной ползучести того же типа тензорезисторов, исследованных в атмосферных условиях. Кратковременная ползучесть материалов , неодинаково сопротивляющихся растяжению - сжатию. Кривая кратковременной ползучести описывается логарифмической функцией. Для металлов такая зависимость объясняется с позиции дислокационной теории8 и хорошо подтверждается опытом. Для пластмасс зависимость деформации от времени при больших значениях деформаций, например при деформировании материалов, близких по свойствам к резине, не подчиняется логарифмическому закону. Разрыв при кратковременной ползучести тесно связан с процессом ползучести, однако при этом зависимость напряжений и температуры от времени такова, что элемент разделяется на две части. При этом напряжения и температура, как правило, таковы, что период установившейся ползучести очень непродолжителен или совсем отсутствует. Испытания на кратковременную ползучесть проводятся по методу изготовителя, согласованному в установленном порядке. Представляется существенным исследование кратковременной ползучести при нестационарных режима х нагружения - в условиях переменных нагрузок и температур, близких к условиям работы реальных конструкций. Специфика испытаний на кратковременную ползучесть обусловлена характером нагружения и нагрева некоторых конструктивных элементов. Решающее значение в этом случае приобретают мгновенные пластические деформации и переходная стадия ползучести. С помощью соотношения можно также предсказать разрыв при кратковременной ползучести , если величины Lt соответствуют такому разрыву. Описанный метод расчета дает относительно точные результаты, если величина деформации при ползучести определяется в основном стадией II установившейся ползучести. В других случаях метод может привести к ошибочным результатам. Много времени и усилий было затрачено на разработку методологии проведения таких испытаний на кратковременную ползучесть, по результатам которых можно было бы точно и надежно прогнозировать поведение материалов при длительной ползучести и их разрушение в условиях ползучести. По-видимому, однако, действительно надежные данные могут быть получены лишь с помощью проведения испытаний на длительную ползучесть, при которых, насколько это возможно, воспроизводятся эксплуатационные нагрузки и температурные условия. |
54. Неустановившаяся и установившаяся ползучесть Неустановившейся ползучестью называется ползучесть, протекающая при изменяющихся во времени напряжениях. Если напряжения во времени постоянны, то этот процесс называется установившейся ползучестью. Установившаяся ползучесть имеет место в случае статически определимых задач при постоянных во времени внешних силах. Это объясняется тем, что в таких задачах напряжения определяются только уравнениями статики, а поскольку внешние силы постоянны, напряжения во времени также не изменяются. Так, например, в образце, растянутом постоянной во времени силой при малых деформациях, когда можно пренебречь изменением площади поперечного сечения, напряжения во времени не изменяются. Точно так же в тонкостенной трубке, нагруженной внутренним давлением, растягивающей силой и крутящим моментом при постоянных нагрузках и малых деформациях, напряжения во времени не изменяются. В статически неопределимых задачах для вычисления напряжений необходимо добавочно рассматривать деформации, которые изменяются во времени вследствие ползучести материала. Поэтому в таких задачах даже при постоянных во времени внешних силах и малых деформациях изменение деформаций всегда связано с изменением напряжений и перераспределением их по объему детали. Если при решении этих задач приближенно предположить, что напряжения во времени постоянны, то получающиеся напряжения и закон распределения их отличны от таковых в начальный момент времени, когда деформаций вследствие ползучести еще не было. Но процесс изменения напряжений во времени остается невыясненным. В действительности, как показали исследования неустановившейся ползучести, напряжения непрерывно изменяются во времени, все более и более приближаясь к величинам, полученным при решении задачи установившейся ползучести. Таким образом, распределение напряжений при установившейся ползучести является как бы предельным. После некоторого промежутка времени распределение напряжений близко к установившемуся. При решении задач неустановившейся ползучести условиям совместности деформаций должны удовлетворять компоненты полных деформаций.
Рис. 4.1. Статически неопределимая стержневая система При решении задач установившейся ползучести упругими деформациями по сравнению с деформациями ползучести можно пренебречь (это справедливо для достаточно больших значений времени), и условиям совместности деформаций должны удовлетворять компоненты деформаций ползучести. Для того чтобы наглядно проиллюстрировать установившуюся и неустановив- шуюся ползучесть, рассмотрим упругое и чисто пластическое состояния, а также состояния установившейся и неустановившейся ползучести для двух стержней ВВ, и СС, одинаковой длины I, одинаковой площади поперечного сечения F и из одинакового материала, соединенных при помощи жесткой плиты АВС, шарнирно закрепленной в точке А. Вес плиты Р (рис. 4.1). Основными уравнениями для рассматриваемой задачи является уравнение равновесия, которое может быть представлено в виде
где а, и <т2 —
напряжения в первом ВВ, и втором СС, стержнях
соответственно; s = P/F, а также уравнение совместности
деформаций Решив задачу в пределах упругости, установим напряжения в стержнях: σ1 = S/5; σζ = 2s/5. При чистопластическом
состоянии системы (если упрочнение отсутствует) напряжения в стержнях
одинаковы, и из уравнения (4.1) следует, что
Для определения напряжений с учетом ползучести материала продифференцируем равенство (4.2) по времени, получая таким образом условие совместности скоростей деформаций
Положим, что пластические деформации отсутствуют, и представим скорость деформации в виде суммы скоростей упругой деформации Iе и деформации ползучести, используя для первой закон Гука, а для второй—степенную зависимость от напряжения (1.2): Этот же результат можно получить, если значения деформаций ползучести по формуле (1.10) подставить в условие совместности деформаций (4.2). Из соотношений (4.6) при п — 1 находим напряжения в пределах упругости, а при п — оо — напряжения в чистопластическом состоянии. Обратим внимание на то, что между полученными выше решениями существует следующая связь:
где & = 5 G~- 1 )/(г~ + 1).
Преобразуем условие совместности скоростей деформаций, принимая во внимание формулу (4.7): Если считать ползучесть установившейся, т. е. предполагать, что напряжения во времени не изменяются, то первое слагаемое в выражении (4.4) равно нулю, и из условия совместности скоростей деформаций (4.3) следует
Решим задачу неустановившейся ползучести, используя теорию течения в формулировке (2.4) и предполагая, что напряжения в стержнях меньше предела пропорциональности материала при данной температуре. Согласно формуле (2.4) скорость полной деформации
Из уравнения равновесия (4.1) вытекает, что ar — s — 2а2 и, следовательно, поскольку сила Р и величина s постоянны во времени, = —2 Подставим эти величины а, и - в уравнение (4.8). После преобразований получается дифференциальное уравнение для <т2:
Введем безразмерные напряжение а2 и время (*:
Тогда уравнение (4.9) принимает вид
Проинтегрируем это уравнение, учитывая, что в начальный момент времени σ2 (0) = 2s/5; σ2(0) = 2/5:
где ζ — переменная интегрирования. На рис. 4.2 представлены графики зависимостей σ1* от t* и σ2* от t*,построенных по формулам (4.10) и (4.1) при п = 3, из которых следует, что с течением времени напряжения изменяются от начального упругого состояния до установившегося. Таким образом, поскольку расчеты с допущением, что ползучесть установившаяся, значительно проще, чем без него, можно, если срок службы детали достаточно велик, предполагать ползучесть установившейся. Однако в тех случаях, когда необходимо исследовать изменение и перераспределение напряжений во времени, как, например, в задаче о релаксации контактного давления в диске, посаженном на вал с натягом, предположение, что ползучесть установившаяся, не может быть принято. Зависимости компонентов скоростей деформации ползучести от компонентов напряжений в условиях установившейся ползучести можно получить из соотношений (3.23), полагая скорости изменения напряжений равными нулю:
Интегрируя эти уравнения по времени и принимая во внимание, что напряжения во времени постоянны, получаем
Такие же соотношения следуют из пренебречь упругими деформациями
Рис. 4.2. Зависимость безразмерных напряжений от безразмерного времени зависимостей (3.12), если по сравнению с деформациями ползучести. Таким образом, допущение о постоянстве напряжений во времени равносильно пренебрежению упругими деформациями по сравнению с деформациями ползучести. Зависимость интенсивности деформаций ползучести от напряжения может быть принята такой же, как и в теории старения, т. е. (3.13). В случае постоянных во времени напряжений она следует также из степенной зависимости интенсивности скоростей деформаций ползучести от интенсивности напряжений (3.25), принятой в теории течения. Таким образом, при установившейся ползучести вывод зависимостей компонентов деформаций ползучести от компонентов напряжений не связан с использованием теорий ползучести. Поскольку в решениях задач установившейся ползучести условиям совместности деформаций должны удовлетворять компоненты деформаций ползучести, определяемые формулами (4.11), эти решения эквивалентны расчетам при нелинейных зависимостях между напряжениями и деформациями. В частности при использовании зависимости (3.13) они эквивалентны решениям чистопластических задач со степенным упрочнением |
|||||||||||||||||||||||||||||||
|
55.Длительная прочность при неодноостном напряженном состоянии
|
Шпоры по теории ползучестиТехнические теории ползучести. Основные понятия.
Теория старения. Теория упрочнения. Теория течения. | |||||||||||||||||||||||
|
Текст:
| |||||||||||||||||||||||
|
|
||||||||||||||||||||||













 .
Полученное дифференциальное уравнение теории течения справедливо при не
слишком малых скоростях ползучести и медленно изменяющихся напряжениях,
достаточно больших в начале процесса. Оно нашло применение в расчетах
металлических узлов и соединений при высоких температурах.
.
Полученное дифференциальное уравнение теории течения справедливо при не
слишком малых скоростях ползучести и медленно изменяющихся напряжениях,
достаточно больших в начале процесса. Оно нашло применение в расчетах
металлических узлов и соединений при высоких температурах. .. Теория
упрочнения удовлетворительно описывает ползучесть при не очень сложных
законах изменения внешних нагрузок.
.. Теория
упрочнения удовлетворительно описывает ползучесть при не очень сложных
законах изменения внешних нагрузок. . Они
описываются схожими интегральными уравнениями. В теории старения механические
характеристики принимаются зависящими от возраста материала.
. Они
описываются схожими интегральными уравнениями. В теории старения механические
характеристики принимаются зависящими от возраста материала.
 ;
;  - определяет
деформацию ползучести при единичном напряжении σ = 1;
- определяет
деформацию ползучести при единичном напряжении σ = 1;  .
.
 указывает
на приращение деформации от напряжения
указывает
на приращение деформации от напряжения  за
время
за
время  .
.


 или
или 






 на
на




 принимает
следующее предельное значение:
принимает
следующее предельное значение:



























































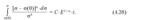












































































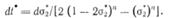





 (zip - application/zip)
(zip - application/zip)










