ЦЕПЬ МАРКОВА С ЧАСТИЧНЫМИ СВЯЗЯМИ И ПЕРЕМЕННЫМ ШАБЛОНОМ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

Кафедра математического моделирования и анализа данных

ЦЕПЬ МАРКОВА С ЧАСТИЧНЫМИ СВЯЗЯМИ И ПЕРЕМЕННЫМ ШАБЛОНОМ

Курсовая работа

Батуры Олега Владимировича

студента 3 курса,

специальность

«Компьютерная безопасность»

Научный руководитель:

доктор физ.-мат. наук,

заведующий кафедрой ММАД

Ю. С. Харин

Минск, 2015

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ПРИКЛАДНОЙ математики и информатики

Кафедра математического моделирования и анализа данных

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Студент Батура Олег Владимирович, 3 курс, 9 группа

1.   Тема работы Цепь Маркова с частичными связями и переменным шаблоном

2.   Срок сдачи студентом законченной работы ________ 2015 г.

3.   Перечень вопросов, подлежащих разработке

·        Исследовать вероятностные характеристики модели цепи Маркова с частичными связями и переменным шаблоном. Найти -мерное распределение вероятностей .

·        Построить компьютерную модель ЦМ с переменным шаблоном.

·        Построить статистические оценки параметров модели при известной функции шаблона , исследовать свойства оценок.

·        Построить оценки параметров модели при периодически изменяющемся, но неизвестном шаблоне.

Руководитель курсовой работы______________ / Ю. С. Харин/ ______ 2015 г.

Задание принял к исполнению_______________ 2015 г.

ОГЛАВЛЕНИЕ

Введение. 4

1.   ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 5

1.1.   Цепь Маркова порядка . 5

1.2.   Цепь Маркова с частичными связями ЦМ. 7

1.3.   Цепь Маркова с частичными связями и переменным шаблоном ЦМ  9

1.4.   Статистическое оценивание параметров ЦМ, состоятельность оценок  11

1.5.   Статистическое оценивание параметров ЦМ. 15

2.   ПРАКТИЧЕСКАЯ ЧАСТЬ. 16

2.1.   Описание программы.. 16

2.2.   Моделирование временного ряда длительности . 17

2.3.   Построение оценок максимального правдоподобия  и . 18

2.4.   Результаты экспериментов. 21

2.5.   Вывод. 23

Заключение. 24

Список использованной литературы.. 25

Введение

При математическом моделировании сложных систем и процессов в различных научных сферах часто возникает необходимость построения вероятностно-статистических моделей дискретных временных рядов 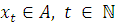, где пространство состояний  — конечное множество мощности  с длинной памятью [1]. Известной моделью таких дискретных временных рядов является цепь Маркова достаточно высокого порядка , определяющего длину памяти; если , то цепь Маркова называется простой, если  — сложной. Однако для такой модели число параметров  растет экспоненциально при увеличении порядка : , и для статистического оценивания параметров требуется иметь реализацию  не всегда доступной на практике длительности . В связи с этим актуальна проблема построения малопараметрических моделей цепей Маркова высокого порядка. В данной работе исследуется малопараметрическая модель цепи Маркова порядка  с  частичными связями ЦМ, рассмотренная в [2], для которой шаблон связей  зависит от времени, исследуются ее вероятностные характеристики, строятся статистические оценки параметров при известной функции шаблона, а также при периодически изменяющемся, но неизвестном шаблоне.

1.    ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1.         Цепь Маркова порядка

В криптологии для моделирования дискретных временных рядов с глубиной памяти  используется цепь Маркова порядка  (ЦМ), обобщающая модель простой цепи Маркова [3].

Определение. Цепь Маркова , порядка  с пространством состояний , определенная на вероятностном пространстве () и временной области , характеризуется обобщенным марковским свойством:

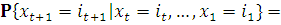
Это означает, что условное распределение вероятностей будущих состояний при фиксированной предыстории зависит не от всей этой предыстории, а от ближайшей на глубину  предыстории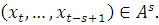

Цепь Маркова ЦМ() характеризуется -мерным начальным распределением вероятностей

и -мерной матрицей вероятностей одношаговых переходов в момент времени :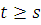

=

Матрица  при этом удовлетворяет условиям нормировки (если она не зависит от времени, то есть , ЦМ() в таком случае называется однородной):

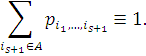
В таком случае -мерное распределение вероятностей имеет вид:

Число независимых параметров, определяющих матрицу вероятностей одношаговых переходов  для однородной ЦМ(), равно             .

При увеличении глубины памяти  число параметров экспоненциально возрастает, и для идентификации такой модели требуется наблюдать реализацию  не всегда доступной на практике длительности .

Возникает задача поиска малопараметрической модели цепи Маркова высокого порядка, для которой число параметров в матрице  задается числом параметров . Одной из таких моделей является цепь Маркова порядка  с  частичными связями (ЦМ) [2].

1.2.         Цепь Маркова с частичными связями ЦМ

Пусть   – однородная ЦМ(), заданная на вероятностном пространстве () с некоторой ()-мерной матрицей вероятностных переходов

Рассмотрим  – параметр, который называется числом связей;  – произвольный целочисленный -вектор с упорядоченными компонентами:

Этот вектор называется шаблоном связей,  – множество всевозможных таких векторов с  компонентами, мощность                                          – некоторая -мерная стохастическая матрица.

Определение. Цепь Маркова  называется цепью Маркова -го порядка с -частичными связями и обозначается ЦМ(), если ее вероятности одношаговых переходов имеют вид:

Это означает, что вероятность перехода процесса в состояние  в момент времени  зависит не от всех  значений предыдущих состояний процесса, а лишь от некоторых   избранных состояний.

В данном случае, вместо  параметров ЦМ() данная модель полностью определяется параметрами , что играет существенную роль на практике.

Замечание. Если , , то  и ЦМ() представляет из себя цепь Маркова порядка , то есть ЦМ( ЦМ.

В дальнейшем будем рассматривать однородную цепь Маркова с частичными связями.

Следует отметить, что -мерное распределение вероятностей для данной модели имеет следующий вид:

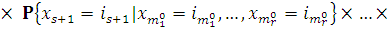
Возникает проблема исследования свойств такой модели цепи Маркова, в которой шаблон зависел бы от какой-либо функции. Данное свойство помогло бы сделать распознавание шаблона для злоумышленника более проблематичным, что сыграло бы важную роль в криптостойкости модели.

1.3.         Цепь Маркова с частичными связями и переменным шаблоном ЦМ

Пусть  – однородная ЦМ(), заданная на вероятностном пространстве (), определенная ранее. Рассмотрим обобщение данной модели, когда шаблон зависит от времени :

причем:

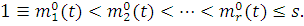
          В общем случае шаблон зависит от некоторой функции, определяющей его изменение. Простейшая модель такой зависимости – периодическая функция с некоторым периодом :

.

          В частности, при 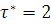 имеются два различных шаблона  и  которые циклично повторяются:

          Для данного частного случая -мерное распределение вероятностей имеет вид:

          При произвольной модели зависимости шаблона от времени имеем общую формулу:

          Использование такой модели цепи Маркова позволяет сделать выборку для злоумышленника как можно более случайной, что сильно влияет на криптостойкость модели, так как появляются сложности с распознаванием зависимости и поиском используемого шаблона. Полезно исследование такой модели ЦМ, в которой шаблон периодически изменяется, но неизвестен.

          Далее рассмотрим задачу статистической оценки параметров модели ЦМ при известном шаблоне и поиска свойств оценок.

1.4.         Статистическое оценивание параметров ЦМ, состоятельность оценок

Для статистического оценивания параметров ЦМ() будем пользоваться методом максимального правдоподобия.

Рассмотрим задачу построения оценок максимального правдоподобия (ОМП) для параметров  шаблона  и  стохастической матрицы 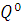 по наблюдаемой реализации  длительности .

          Введем обозначения, пусть  – мультииндекс -го порядка;  – функция, которую назовем селектором -го порядка с параметрам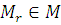и  и    – индикатор события ; – начальное -мерное распределение вероятностей ЦМ;

– частота -граммы  для шаблона , удовлетворяющая условию нормировки:

          Для модели ЦМ логарифмическая функция правдоподобия имеет вид:

          Для того, чтобы найти ОМП для матрицы 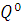, необходимо решить задачу на условный экстремум:

          В результате получаем условную ОМП для матрицы  ():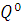

          Далее рассматривается задачу поиска ОМП для шаблона .

          Пусть  – стационарное распределение вероятностей ЦМ. Пусть ЦМ – стационарна (), тогда распределение вероятностей -граммы для шаблона  будет иметь следующий вид:

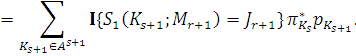
          Соответствующая частотная оценка вероятностей:

.

          Энтропия -мерного распределения вероятностей запишется в виде:

          Количество информации по Шеннону, содержащейся в -грамме  о будущем символе :

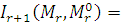
Логарифмическая функция правдоподобия для оценки имеет следующий вид:

где  – подстановочная оценка энтропии, получающаяся при подстановке вместо истинных значений 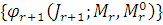 их оценок {}.

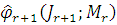Учитывая, что  не зависит от , добавляя также не зависящее от  слагаемое , а также используя тот факт, что:

приходим к следующей ОМП шаблона :

где  – подстановочная оценка количества информации по Шеннону, получающаяся при подстановке вместо истинных значений 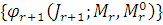 их оценок {}.

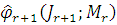Теорема 1. Если ЦМ является стационарной, то при истинном шаблоне  и  оценка  состоятельна:

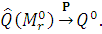
Теорема 2. Если ЦМ является стационарной и шаблон  идентифицируемый, то при  оценка  состоятельна:

1.5.         Статистическое оценивание параметров ЦМ

Для ЦМ оценки параметров генератора с переменной обратной связью строятся аналогично модели с постоянной обратной связью с учетом периодически изменяющегося шаблона .

Логарифмическая функция правдоподобия имеет следующий вид:

            Задача на условный экстремум

решается в общем виде, и это позволяет решить частную задачу оценки параметров генератора с переменной обратной связью.

Теорема 3. Если ЦМ является стационарной, то при истинном шаблоне  и  оценка  состоятельна:

Теорема 4. Если ЦМ является стационарной и шаблон  идентифицируемый, то при  оценка  состоятельна:

2.    ПРАКТИЧЕСКАЯ ЧАСТЬ 2.1.         Описание программы

Построена компьютерная модель цепи Маркова с частичными связями и переменным шаблоном со следующими входными параметрами:

·         глубина предыстории однородной цепи Маркова ЦМ.

·        длина временного ряда с пространством состояний .

·        Шаблоны  и , которые повторяются с периодом

·        Стохастическая матрица вероятностей одношаговых переходов для шаблонов:

          В частном случае, при  данная матрица имеет следующий вид:

Реализовано моделирование цепи Маркова с частичными связями и переменным шаблоном, нахождение оценок максимального правдоподобия матрицы вероятностей одношаговых переходов  и переменного шаблона  смоделированного временного ряда. Далее более подробно рассматривается алгоритм работы программы.

2.2.         Моделирование временного ряда длительности

Случайным образом выбираются первые  элементов последовательности. Для моделирования элементов  с нечетными номерами  выбирается шаблон . Рассматривается -предыстория элемента. Распределениями вероятностей исхода для данных элементов являются строки матрицы 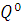, соответствующие состояниям предыдущих элементов

В частности, если предыстория элемента  имеет вид

,

то при

Элементы  с четными номерами  моделируются аналогичным образом с использованием шаблона

На каждом шаге моделирование происходит с помощью генератора псевдослучайных чисел, работающего по следующему алгоритму:

1.     Генерируется число  в диапазоне .

2.    

В результате имеется временной ряд , где пространство состояний  – конечное множество мощности .

2.3.         Построение оценок максимального правдоподобия  и

Логарифмическая функция правдоподобия имеет вид:

Задача на условный экстремум:

Поиск условной оценки максимального правдоподобия матрицы одношаговых переходов  ищется путем приравнивания к нулю компонент градиента логарифмической функции правдоподобия:

Используя тот факт, что матрица  стохастическая,

, условная оценка  полностью определяется шаблоном

Для вычисления оценки  шаблона  при известном истинном значении числа связей  можно воспользоваться алгоритмом полного перебора  значений логарифмической функции правдоподобия.

В частности, при  имеется следующая система уравнений:

где  частота выпадения  при предыстории .

Условной оценкой максимального правдоподобия  является решение данной системы:

.

Логарифмическая функция правдоподобия перепишется в следующей форме:

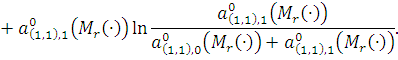
Оценка максимального правдоподобия  ищется путем перебора  вариантов шаблонов. Производится подсчет частот  при всевозможных вариантах пар шаблонов и выбирается та пара, которая максимизирует логарифмическую функцию правдоподобия. Таким образом:

Оценка максимального правдоподобия матрицы 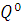 имеет вид:

2.4.         Результаты экспериментов

Экспериментальные оценки параметров построены при следующих входных данных:

Рис. 1. Зависимость числа ошибок распознавания истинного шаблона  при 100 экспериментах от

При :

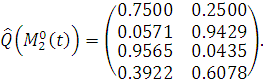
При :

При :

При :

2.5.         Вывод

Результаты показывают состоятельность оценки  при истинном шаблоне  и . Также очевидна состоятельность оценки шаблона  при .

Таким образом, для более точного распознавания матрицы одношаговых переходов 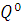 и шаблона  требуется наблюдать реализацию как можно большей длительности .

Заключение

В данной работе исследованы вероятностные характеристики модели цепи Маркова с частичными связями и переменным шаблоном, реализована компьютерная модель ЦМ с переменным шаблоном. Построены статистические оценки параметров модели при известной функции шаблона , периодически изменяющемся, но неизвестном шаблоне. Исследована состоятельность данных оценок.

Результаты экспериментов показали, что для более точного распознавания матрицы одношаговых переходов 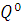 и шаблона  требуется наблюдать реализацию как можно большей длительности .

Список использованной литературы

1.     Алферов А. П. и др. Основы криптографии / Алферов А. П., Зубов А. Ю., Кузьмин А. С., Черемушкин А. В. – 2-е изд., испр. и доп. – М.: Гелиос АРВ, 2002. – 480 с.

2.     Харин Ю. С., Петлицкий А. И. Цепь Маркова -го порядка с  частичными связями и их статистическое оценивание – Дискретная математика, 2007. – Т. 12, вып. 2. С. 109-130.

3.     Харин Ю. С. и др. Криптология / Харин Ю. С., Агиевич С. В., Васильев Д. В., Матвеев Г. В. – Мн.: БГУ, 2013. – 511 с.