Розробка практичного модуля дистанційного курсу Додаткові розділи дискретної математики

Міністерство освіти і науки України

Рівненський державний гуманітарний університет

Кафедра інформаційно-комунікаційних технологій та МВІ

КУРСОВА РОБОТА

з інформатики

на тему:

Розробка практичного модуля дистанційного курсу «Додаткові розділи дискретної математики»

Студента ІV курсу групи МІ-42

напряму підготовки 6.040201

«Математика»

спеціальності вчитель математики і інформатики

Махна Артура Сергійовича

Керівник: доц. Павелків О.М.

                                                       Національна шкала ________________

Кількість балів: ________Оцінка: ECTS _____

                                    Члени комісії _____________   ______________________

(підпис)                      (прізвище та ініціали)

                                                            _____________   ______________________

(підпис)                      (прізвище та ініціали)

                                                            _____________   ______________________

(підпис)                      (прізвище та ініціали

м.Рівне – 2015р.

ЗМІСТ

ВСТУП ……………………………………………………………………...................3

РОЗДІЛ 1. НАУКОВО-ТЕОРЕТИЧНІ ОСНОВИ ДОСЛІДЖЕНЬ …………….......6

1.1.         Теоретичні основи лінійних рівнянь та їх систем ....……………….....6

РОЗДІЛ 2. МЕТОДИКА ВИВЧЕННЯ ЛІНІЙНИХ РІВНЯНЬ ТА ЇХ СИСТЕМ У КУРСІ 7 КЛАСУ……………………………………………………………………..23

2.1.         Лінійне рівняння з однією змінною…………………………..……..…23

2.2.         Лінійне рівняння з двома змінними…………………………..………..24

2.3.         Графік лінійного рівняння з двома змінними…………………………

2.4.         Система двох лінійних рівнянь з двома змінними……………..

ВИСНОВОКИ ………………………………………………………...…….....30

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ……………….………………....32

ВСТУП

Необхідність розв"язувати рівняння ще в давнину була викликана потребою розв"язувати задачі, пов"язані із знаходженням площі земельних ділянок і з земельними роботами військового характеру, а також із розвитком астрономії і самої математики. Рівняння вміли розв"язувати близько 2000 років до н.е. вавилоняни. Використовуючи сучасний алгебраїчний запис, можна говорити, що в їх клинописних текстах зустрічаються, крім неповних, і такі, наприклад, повні квадратні рівняння: х² + х = , х² - x = 14

Правило розв"язування цих рівнянь, викладене у вавилонських текстах, співпадає суттєво із сучасним, хоча невідомо, яким чином дійшли вавилоняни до цього правила. Майже всі знайдені до цього часу клинописні тексти наводять лише завдання з розв"язками, викладеними у вигляді рецептів, без вказівок відносно того, яким чином вони були знайдені.

Задачі на квадратні рівняння зустрічаються вже в астрономічному тракті. "Аріабхаттіам", що був складений в 499 році індійським математиком і астрономом Аріабхаттою. Інший індійський вчений Брахмагупта (VII ст.) виклав загальне правило розв"язування квадратних рівнянь, зведених до єдиної канонічної форми:

ах² + bх = с, а > 0.         (1)

У рівнянні (1) коефіцієнти, крім "а", можуть бути і від"ємними. Правило Брахмагупти суттєво співпадає з теперішнім.

XVI ст. в Італії характеризувалося специфічними звичаями в науковому житті. Право на професорську посаду та пріоритети різного роду відкриттів тоді захищалися на публічних наукових диспутах, які часто перетворювалися на азартні турніри. За цих умов деякі вчені довгий час тримали в таємниці свої відкриття. Найбільша суперечка того часу виникла між італійськими математиками Н. Тарталья і Д. Кардано за пріоритет відкриття правила розв"язання кубічного рівняння.

Формули розв"язування квадратних рівнянь за зразком аль-Хорезмі в Європі були вперше викладені в "Книзі абака", написаної в 1202 році італійським математиком Леонардо Фібоначі. Задачі з "Книги абака" переходили майже в усі європейські підручники ΧVΙ – ΧVΙΙ ст. і частково ΧVΙΙΙ.

Мета: комплексно вивчити та дослідити систему алгебраїчних рівнянь.

Завдання дослідження:

1.     Проаналізувати лінійні системи рівнянь.

2.     Дослідити однорідні системи рівнянь.

3.     Охарактеризувати симетричні системи рівнянь.

4.     Дослідити алгебраїчні системи рівнянь вищих степенів та їх рівняння із застосуванням результантів.

Об’єкт дослідження: лінійна алгебра.

Предмет дослідження: система алгебраїчних рівнянь.

Методи дослідження. В процесі написання курсової роботи нами буливикористані такі методи: аналіз, порівняння, узагальнення, класифікація та систематизація даних науково-методичних, довідкових джерел.

Обсяг і структура роботи обумовлені метою та завданнями дослідження, а також логікою розташування в ній матеріалу. Курсова робота складається із вступу, чотирьох розділів, висновків та списку використаної літератури.

Упродовж багатьох століть алгебра розвивалась як наука про рівняння.

Основні відомості про рівняння ми вже могли дізнатися із попередніх класів. Нагадаємо, що вираз, записаний в рівнянні ліворуч від знака рівності, називають лівою частиною рівняння, а ви­раз, записаний праворуч, - правою частиною рівняння. Якщо в рівняння 4х - 6 = х замість змінної х підставити число 2, то одержимо правильну числову рівність 4 • 2 - 6 = 2, оскільки числові значення обох частин рівняння стануть між собою рів­ними. У такому разі про число 2 кажуть, що воно задовольняє рівняння, тобто с його коренем.

Рівняння можуть мати різну кількість коренів. Наприклад, рівняння 4х - 6 = х мас лише один корінь число 2. Рівняння х(х - 6) = 0 мас два корені числа 0 і 6. Будь-яке значення змінної х задовольнятиме рівняння х + 0,1 = 0,1 + х, тому будь-яке число є його розв’язком, отже, це рівняння мас безліч коренів. Але не існує жодного значення змінної х, яке б пере­творювало рівняння х + 1 = х у правильну числову рівність, оскільки при кожному значенні змінної х значення лівої час­тини рівняння буде па 1 перевищувати значення правої його частини. Тому рівняння х - 1 = х не мас коренів.

Розглянемо рівняння х + 1 = 5 і 3х = 12. Кожне з них мас єдиний корінь число 4. Ці рівняння с рівносильними.

Приклад 1. З’ясувати, чи с рівносильними рівняння:

1)            18 - х = 11  і  21 : х = 3;       

2)            2) х + 3 = х  і  2 - х = 5 - х;

1)            х + 3 = 4  і  5х - 10?

Розв’язання.  

1.     Коренем рівняння 18 - х = 11 с чис­ло 7. Коренем рівняння 21 : х = 3 також с число 7. Тому рівняння 18- х = 11 і 21: х = 3 - рівносильні.

2.     Обидва рівняння х + 2 = х  і  2 - х = 5 - х не мають коре­нів, тому є рівносильними.

3.     Коренем рівпяппя х + 3 = 4 с число 1, а коренем рівняння 5х = 10 – число 2. Тому рівняння х + 3 = 4 і 5х = 10 не є рівно­сильними.

Під час розв’язування рівнянь використовують властивос­ті, які перетворюють рівняння па рівносильні їм рівняння:

Приклад 2. З’ясувати, чи с рівносильними рівняння:

1.      2(х - 1) = 5х і 2х - 2 = 5х;

2.     3а + 2 = 5а - а - 7  і 3а + 2 = 4а - 7;

3.     5х = 2х + 9 і 5х - 2х = 9;

4.     0,5b = 1,5b - 3,5 і b = 3b - 7.

Розв’язання.

1.     Рівняння 2(х - 1) = 5х і 2х - 2 = 5х є рівносильними, оскільки друге рівняння одержуємо з першого розкриттям дужок у його лівій частині.

2.     Рівняння 3а + 2 = 5а - а - 7  і 3а + 2 = 4а - 7 - рівно­сильні, оскільки друге рівняння одержуємо з першого зведен­ням подібних доданків у його правій частині.

3.     Рівняння 5х = 2х + 9 і 5х - 2х = 9 - рівносильні, оскіль­ки друге рівняння одержуємо з першого перенесенням додатка з правої частини рівняння в ліву із зміною знака цього додатка па протилежний.

4.     Рівняння 0,5b = 1,5b - 3,5 і b = 3b - 7 - рівносильні, оскільки друге рівняння одержуємо шляхом множення на 2 обох частин першого рівняння.

У IX ст. видатний арабський математик Мухаммед бен Муса аль-Хорезмі у своєму трактаті «Кітаб аль-джебр аль-мукабала» зі­брав і систематизував існуючі на той час ме­тоди розв"язування рівнянь. Узятий з назви цієї книжки термін «аль-джебр» (у перекладі з арабської означає «відновлення») надалі почав уживатися як «алгебра» і дав назву цілій науці.

У ті часи, коли аль-Хорезмі писав свій трактат, від"ємні числа вва­жалися хибними, несправжніми. Тому коли від"ємне число перено­сили з однієї частини рівняння в іншу, змінюючи його знак, вважали, що воно «відновлюється» (стає додатним), тобто з несправжнього перетворюється на справжнє. Саме таке перетворення рівнянь аль-Хорезмі і назвав «відновленням».

Властивість взаємного знищення однакових доданків рівняння, що містилися в обох його частинах, аль-Хорезмі назвав «протиставлен­ням» (арабською мовою - «аль-мукабал»).

Аль-Хорезмі був перший учений, хто відо­кремив алгебру від арифметики і розглянув її як окрему математичну науку. Алгебру аль- Хорезмі в латинському перекладі вивчали євро­пейці протягом XII—XVI ст. Подальший розвиток алгебри пов’язаний саме з європейськими вче­ними. зокрема з італійськими математиками епохи Відродження.

До XIX ст. алгебра розвивалася як наука, що вивчає методи розв"язування рівнянь. Згодом вона значно збагатилася новими змістовими лініями: спрощення виразів, функції, розв"язу­вання нерівностей тощо, і тепер рівняння - це  лише одна зі складових частин алгебри.

Лінійним рівнянням з однією змінною називають рівняння виду , де х – змінна, а і b – числа.

     Якщо а≠0, то рівняння  має єдиний корінь .

    Наприклад: рівняння 5х=6 має корінь х=1,2.

     Якщо а=0, b≠0, то рівняння  не має коренів.

    Наприклад: рівняння 0х=5 не має коренів.

     Якщо а=0, b=0, то коренем рівняння  є будь-яке число.

     Деякі рівняння зводяться до розв’язування лінійних рівнянь. Розглянемо приклади.

    Приклад 1. Розв’яжіть рівняння .

Розв’язання

     Щоб позбутися знаменників дробів, помножимо кожний член рівняння на найменший спільний знаменник дробів, тобто на 20, і отримаємо:

,

40-5(3х-4)+4(х+18)=0.

     Розкриємо дужки:

40-15х+20+4х+72=0.

     Залишимо члени зі змінними в лівій частині рівняння, а члени без змінних перенесемо в праву частину (змінивши знаки членів на протилежні):

-15х+4х=-40-20-72.

     Зведемо подібні доданки:

-11х=-132, звідси х=-132:(-11), х=12.

     Відповідь: 12.

    Приклад 2. Розв’яжіть рівняння (2х-6)(х+2)=0.

Розв’язання

     Якщо добуток кількох множників дорівнює нулю, то хоча б один із множників дорівнює нулю.Скористаємося цим фактом при розв’язуванні даного рівняння.

     Ліва частина рівняння – добуток невідомих множників 2х-6 і х+2, а права частина – нуль. Щоб розв’язати це рівняння, досить прирівняти до нуля множники 2х-6 і х+2 та розв’язати отримані рівняння. Отже, 2х-6=0 або х+2=0, тоді 2х-6=0, 2х=6, х=6:2, х=3 або х+2=0, х=-2.

     Відповідь: 3, -2.

    Приклад 3. Розв’яжіть рівняння .

Розв’язання

     Згадаймо значення модуля:

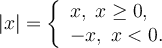
     Із точки зору геометрії |х| означає відстань від точки х, зображеної на координатній прямій, до початку координат (точки 0).

     1-й спосіб.

     Якщо 2х+3<0, то за означенням модуля –(2х+3)=1, тоді 2х+3=-1,  2х=-3-1,  2х=-4, х=-2.

     Якщо 2х+3≥0, то за означенням модуля 2х+3=1, тоді 2х+3=1, 2х=-3+1, 2х=-2, х=-1.

     Відповідь: -1; -2.

     2-й спосіб.

     Ураховуючи геометричний зміст модуля, рівність |2х+3|=1 означає, що відстань від точки 2х+3 до початку координат дорівнює числу 1, тобто

1) 2х+3=-1, 2х=-3-1, 2х=-4, х=-2;

2) 2х+3=1, 2х=-3+1, 2х=-2, х=-1.

     Відповідь: -1; -2.

Лінійним рівнянням з двома змінними  та  називається рівняння виду                          (або виду                          ).

Приклад :

    лінійні рівняння.

Якщо в лівій частині рівняння  і , то це рівняння першого степеня з двома змінними.

Приклад:

 - лінійне рівняння.

 - рівняння першого степеня з двома змінними.

Розв"язком рівняння з двома змінними  і  називається кожна пара чисел ( ; ), яка перетворює це рівняння на правильну числову рівність.

Приклад:

Для рівняння  пара ( 1; 2) є розв"язком, оскільки при  і  одержуємо   - правильна рівність. Пара (0; 1) не є розв"язком заданого рівняння, оскільки при  і 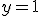 одержуємо ; - неправильна рівність.

Два рівняння з двома змінними називаються рівносильними, якщо вони мають одні й ті самі розв"язки або обидва рівняння не мають розв"язків.

Приклад:

Рівняння  і  - рівносильні.

Властивості рівносильних рівнянь з двома змінними

Якщо обидві частини рівняння з двома змінними помножити або поділити на одне і те саме число, яке не дорівнює нулю, то одержимо рівняння , рівносильне даному.

Приклад :

Рівняння  і  - рівносильні (друге можна одержати з першого множенням на 2).

Якщо будь-який член рівняння з двома змінними перенести з однієї частини рівняння в іншу з протилежним знаком, то одержимо рівняння, рівносильне даному.

Приклад:

Рівняння  і  - рівносильні.

Графік лінійного рівняння з двома змінними

На координатній площині графіком лінійного рівняння   називається множина точок, координати яких задовольняють даному рівнянню.

• Якщо  чи , графіком заданого рівняння є пряма, і для її побудови досить отримати будь - які дві точки цієї прямої.

Приклад :

Графіком рівняння   є пряма 

•  Якщо  і , графіком заданого рівняння є пряма, паралельна  осі 

Приклад :

Графіком рівняння   є пряма 

Якщо  і , графіком заданого рівняння є пряма, паралельна  осі 

Приклад :

Графіком рівняння  є пряма .

 Системи рівнянь розв’язують кількома способами: графічним, підстановки, додавання. Розглянемо приклади.

     Приклад 1. Розв’яжіть систему рівнянь графічним способом 

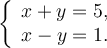
Розв’язання

     Побудуємо графіки рівнянь х+у=5 або у=-х+5 (пряма, яка проходить через точки (0;5) і (5;0)) та х-у=1 або у=х-1 (пряма, яка проходить через точки (0;-1) та (1;0)).

     Ці графіки перетинаються в точці (3;2).

     Отже, розв’язком системи є пара (3;2).

     Відповідь: (3;2).

     Щоб розв’язати систему рівнянь графічним способом, треба:

1. виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;

2. побудувати графіки;

3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв’язками (розв’язком) системи рівнянь.

    Зауваження. Графічний спосіб розв’язування систем рівнянь не є універсальним, оскільки не завжди розв’язком системи є пара цілих чисел. Іноді важко точно встановити координати точки перетину побудованих графіків функцій, можливо лише вказати наближенні значення. Тому, як правило, використовують алгебрагічні способи розв’язування систем рівнянь: спосіб підстановки, додавання.

    Приклад 2. Розв’яжіть систему рівнянь способом підстановки 

Розв’язання

     Із першого рівняння системи виразимо у через х: у=6-2х. одержаний вираз підставимо в друге рівняння системи:

4х-3(6-2х)=2, звідси 4х-18+6х=2; 10х=20; х=2.

     Одержане значення х підставляємо у вираз у=6-2х;

у=6-2·2.

     Отже, пара (2;2) – розв’язок даної системи.

     Відповідь: (2;2).

     Способом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком:

1. з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини;

2. знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;

3. розв’язуємо одержане рівняння і знаходимо значення цієї змінної;

4. підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення;

5. записуємо відповідь.

    Зауваження. Спосіб підстановки, як правило, використовують, якщо коефіцієнт при одній зі змінних в одному з рівнянь системи дорівнює 1.

    Приклад 3. Розв’яжіть систему рівнянь способом додавання 

Розв’язання

     Помножимо почленно перше рівняння системи на 3, а друге – на 2 (це дає змогу при додаванні рівнянь позбавитися від змінної у):

     Додавши почленно рівняння, одержуємо 19х=19, звідси х=1 (значення у знайдемо з першого рівняння системи: 3·1+2у=5, 2у=2, у=1, отже, (1;1) – розв’язок системи).

     Значення у можна знайти, якщо помножимо почленно перше рівняння на -5, а друге – на 3:

     Додавши почленно рівняння, одержуємо:

-19у=-19, у=1.

     Отже, пара (1;1) є розв’язком даної системи.

     Відповідь: (1;1).

     Розв’язування системи двох лінійних рівнянь із двома змінними способом алгебрагічного додавання виконують за таким порядком:

1) урівнюємо коефіцієнти при одній зі змінних шляхом по членного множення обох рівнянь на множники, підібрані відповідним чином;

2) додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну зі змінних;

3) розв’язуємо одержане рівняння з однією змінною;

4) значення другої змінної можна знайти таким же способом (або підстановкою знайденого значення змінної в будь-яке із заданих рівнянь системи);

5) записуємо відповідь.

    Зауваження. Спосіб додавання, як правило, використовують, якщо коефіцієнти при одній зі змінних у рівнянні системи – протилежні числа.

ВИСНОВКИ

Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, та областей фізики й техніки, де застосовуються ці математичні теорії.

Системи лінійних алгебраїчних рівнянь називаються еквівалентними, якщо множина їхніх розв"язків збігається, тобто будь-який розв"язок однієї системи є водночас розв"язком іншої, і навпаки.

Систему, еквівалентну даній, можна отримати, зокрема, замінивши одне з рівнянь на це ж рівняння, помножене на будь-яке відмінне від нуля число. Еквівалентну систему можна отримати також, замінивши одне з рівнянь сумою цього рівняння з іншим рівнянням системи. Загалом, заміна рівняння системи на лінійну комбінацію рівнянь дає систему, еквівалентну початковій.

Сумісна система називається визначеною, якщо вона має єдиний розв"язок, і невизначеною, якщо вона має безліч розв"язків. В останньому випадку кожен її розв"язок називають частковим розв"язком системи. Сукупність усіх часткових розв"язків називають загальним розв"язком системи.

Однорідними називаються многочлени, у яких всі члени мають однаковий сумарний показник степеня. Рівняння з двома невідомими а₀хⁿ + а₁х^n-1 у + а₂х^n-2 у² + …+ а_nхⁿ уⁿ =0 називають однорідним рівнянням.

Фундаментальною системою розв’язків системи однорідних лінійних рівнянь називається така лінійно незалежна сукупність її розв’язків, що всякий розв’язок даної системи є якоюсь лінійною комбінацією розв’язків з цієї сукупності.

Многочлени називаються симетричними, якщо при будь - якій перестановці змінних, що входять до нього дістанемо тотожно рівний йому многочлен. Система рівнянь з п невідомими називаються симетричною, якщо вона не міняється при перестановці змінних.

Методи розв"язання алгебраїчних рівнянь вищих степенів базуються в основному на двох принципах: а) розкладання лівої частини рівняння, права частина якого дорівнює нулю, на множники з наступною заміною вихідного рівняння еквівалентного йому сукупністю рівнянь меншого степеня; б) послідовним пониженням степеня вихідного рівняння або, навіть, зведенням його до квадратного за допомогою вдало підібраної заміни змінних.

СПИСОК ЛІТЕРАТУРИ

1. Богданов И. М.. Петраков И. С. Сборник задач по алгебре. Пособие для учителей. – М.: Просвещение, 1991. – 183 с.
2. Бартенев Ф. А. Нестандартные задачи по алгебре и элементарным функциям. Пособие для учителей. – М.: Просвещение, 1983. – 448 с.
3. Вашук Ф. Г., Поляк С. С. Практикум з алгебри. – Ужгород, 1997.
4. Вишенський В. А., Перестюк М. О., Самойленко А. М. Збірник задач з математики: Навч. посібник. – 2-ге вид., доп. – К.: Либідь, 1993.
5. Вища алгебра. Підручник для вищих навчальних закладів. / Грильков Б. В. /. - Х.: Гімназія, 2003.
6. Ефимов А. Математический анализ (спец. разделы). - М.: Высшая школа, 1980.
7. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. - М.: Наука, 1987.
8. Маркушевич А. И. Теория аналитических функций. - М.: Наука, 1978.
9. Потапов М. К., Олехник С. Н., Нестеренко Ю. В. Математика. Методы решения задач для поступающих в ВУЗы. – М.: Дрофа, 1995.
10. Сидоров Ю. В., Федорюк М. В., Шабунин М. И. Лекции по теории функций комплексного переменного. - М.: Наука, 1982.
11. Смирнов В. И. Курс высшей математики. - М.: Наука, 1974.
12. Овчинников П. П. Вища математика. Підручник для студентів вищих технічних навчальних закладів. У 2 ч. Ч 2. - К.: Техніка, 2004.
13. Радченко О. Т. Математичний аналіз. Ч.2. - К.: ТВ і МС, 2000.
14. Чинаев П. И., Мишин Н. А. и др. Высшая математика. Специальные главы. - К.: Вища школа, 1981.
15. Ципкін О.Г. Довідник з математики для середніх навчальних закладів. - К., 1988.
16. Шарыгин И. Ф., Голубев В. И. Факультативный курс по математики. – М.: Просвещение, 1991.