МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МГУПИ
Курсовая работа по курсу
«Вычислительные системы»
Направление подготовки:
«Информатика и вычислительная техника»
Москва
2015
1. Математические методы оценки эффективности и производительности параллельных вычислительных систем.
Под параллельной системой будем понимать вычислительную систему, состоящую из n одинаковых функциональных устройств, объединённых вычислительной сетью. Рассмотрим решение одной вычислительной задачи A на параллельной системе. Пусть время решения задачи A на этой системе составляет T . Пусть время решения задачи A одним устройством, используя последовательный алгоритм, равно T0 .
Обычно ускорение S определяется как отношение [1]:
S =T0/T
(1)
Таким образом, ускорение показывает, во сколько раз можно уменьшить время решения задачи с помощью применения параллельной системы.
Принято определять эффективность E параллельной системы как E =S/n. Эффективность можно переписать как
E=S/n=T0/nT
(2)
Обозначим p1, …, pn – пиковые производительности функциональных устройств, а p1, …, pn – загруженности функциональных устройств.
Тогда производительность p системы равна
p= (3)
(3)
2. Постановка задачи
Рассмотрим распределённую базу данных, в которой каждый узел логически связан с шестью другими узлами, образуя сеть, состоящую из треугольных ячеек.

Рис. 1. Логическое размещение узлов сети.
Узел будем считать функциональным устройством для целей расчёта эффективности и производительности системы.
Информацию в сети разместим следующим образом: всю базу данных разобьём на n частей и распределим по всем n узлам. И данные в каждом узле разобьём на 6 частей и эти части реплицируем на соседние узлы – одну часть на один узел.
Установим, что к базе данных идут запросы на чтение. Ответ на запрос поступает от одного или нескольких (до семи) узлов одновременно в зависимости от объёма запрошенных данных.
В качестве параметра для расчета возьмем скорость передачи данных.
Все узлы по производительности и загруженности будем считать одинаковыми.
Задача: посчитать производительность и эффективность распределённой базы данных относительно базы данных, расположенной в одном узле.
Обозначим V0 – скорость передачи данных от одного узла базы данных, Р0 – загруженность одного узла при передаче данных.
3. Расчет относительной производительности и эффективности
Посчитаем относительную производительность распределённой базы данных. Пиковые производительности и загруженности узлов равны:
pi= V0, i=1,…,n ; pi= P0, i=1,…,n
Тогда производительность распределённой базы данных равна:
p=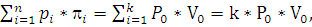
Где k – количество узлов, передающих данные, k=1, …, 7.
Производительность одного узла равна  следовательно, относительная производительность распределённой базы данных равна:
следовательно, относительная производительность распределённой базы данных равна:
p0= , т.е. производительность распределённой базы данных прямо пропорциональна степени её фрагментации.
, т.е. производительность распределённой базы данных прямо пропорциональна степени её фрагментации.
Посчитаем теперь эффективность распределённой базы данных. Начнём с ускорения. Поскольку в формуле (1) фигурирует время, а мы вычисляем эффективность по скорости, зависимость получается обратная:
S=V/V0, где V – скорость передачи данных распределенной базой данных. Причём V=k*V0, откуда следует, что S=k.
Тогда эффективность распределённой базы данных равна:
E=S/n=k/n
Получаем, что, несмотря на высокую производительность, эффективность распределённой системы невелика, особенно при больших значениях n.
Однако мы рассмотрели случай, когда запрос к базе данных всего один. Предположим, что к базе данных одновременно имеются m запросов. И все эти запросы направлены к разным частям распределенной базы данных, т.е. к разным узлам.
Тогда производительность распределённой базы данных будет равна:
p=
где ki=1, …, 7, i=1,…,m.
а относительная производительность
p0=
Фактически, p0 равна количеству узлов, участвующих в ответе на запросы.
В предельном случае, когда к базе данных имеются n запросов, по одному к каждому узлу,
p0=n.
Эффективность равна:
E= /n
/n
В предельном случае, когда к базе данных имеются n запросов, по одному к каждому узлу,
E=1.
4. Выводы
1) Распределённая база данных производительней одноузловой и её производительность пропорциональна количеству узлов, участвующих в передаче данных по запросу.
2) Эффективность распределённой базы данных зависит от её загруженности, т.е. от количества запросов к базе данных и, в пределе, может достигать 1 при условии, что обращение происходит одновременно ко всем узлам.
Литература:
1. Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar Introduction to Parallel Computing, Second Edition. USA: Addison Wesley, 2003.














 (zip - application/zip)
(zip - application/zip)










