Содержание
Введение
3
1 Математические модели при автоматизированном проектировании
технологических процессов
4
2 Математическая модель на основе экспериментально
взвешиваемой силы резания
5
Список литературы
17
Введение
Математическая модель - один из вариантов модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе. Процесс построения и изучения математических моделей называет-ся математическим моделированием.
Все естественные и общественные науки, использующие математичес-кий аппарат, по сути, занимаются математическим моделированием: заменя-ют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математи-ческих методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.
1 Математические модели при автоматизированном
проектировании технологических процессов
Под математической моделью технологического процесса и его элементов понимают систему математических соотношений, описывающих с требуемой точностью изучаемый объект и его поведение в производственных условиях. При построении математических моделей используют различные математические средства описания объекта — теорию множеств, теорию графов, теорию вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и др.
Описание математических соотношений на уровнях структурных, логических и количественных свойств принимает конкретные формы в условиях определенного объекта. Например, множество параметров, влияющих на выбор скорости резания при различных методах обработки, можно представить в виде

где Ти - стойкость инструмента, мин; т — показатель относительной стойкости инструмента; t - глубина резания, мм; s - подача, мм/об(мм/зуб, мм/дв. ход, мм/мин); d — диаметр обрабатываемой поверхности или диаметр инструмента; В — ширина обрабатываемой поверхности, мм; cv — коэффициент, характеризующий условия обработки; kv — поправочный коэффициент на скорость резания; х„, yv9 zv9rv — показатели степени. Логические соотношения между приведенными выше параметрами и скоростью резания v имеют вид

причем Ти, m, cv и kv всегда истинны, а истинные значения других переменных зависят от метода обработки резанием. Формулы количественных соотношений между параметрами с учетом истинности их логарифмических значений имеют вид:
при наружном точении

При сверлении

Следовательно, формулы представленные выше представляют математические модели расчёта скорости резания.
2 Математическая модель на основе
экспериментально взвешиваемой силы резания
Исходные положения. Основу математической модели в рассматриваемом случае составляет банк данных, формируемый по результатам обширных экспериментальных исследований, направленных на взвешивание величины силы резания при планомерно и направленно изменяемых параметрах, составляющих режим резания. В перечень задач для таких исследований входят:
1) анализ системы сил, обеспечивающих резание;
2) разработка техники и технологии для испытаний и экспериментальных измерений, в частности, как силы резания, так и ее составляющих;
3) составление методики экспериментирования для сбора материалов в банк данных;
4) формирование метода графико-аналитической обработки экспериментальных данных;
5) обработка результатов и формирование математической модели процесса резания.
Анализ системы сил. На переднюю поверхность
инструмента действуют некоторая нормальная сила N и сила трения F
сходящей стружки. В результате упругого восстановления поверхности резания на
задней поверхности инструмента аналогично действуют возникающие там нормальная
сила  и сила трения
и сила трения 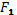 . В совокупности эти силы
уравновешивают силу резания. Распределение давления, действующего на рабочие
поверхности инструмента, показано на рис. 1.
. В совокупности эти силы
уравновешивают силу резания. Распределение давления, действующего на рабочие
поверхности инструмента, показано на рис. 1.
Наибольшее давление Ртах действует вблизи главной режущей кромки (точка 1) По мере удаления от нее давление убывает и в точке 2 равно нулю (здесь прекращается контакт сбегающей стружки с инструментом). На заднюю поверхность лезвия также действует неравномерно распределенная нагрузка, которая максимальна в точке 1, а в точке 3 равна нулю (прекращение контакта задней поверхности лезвия с поверхностью резания), у- передний,
а - задний углы резца.
 |
Рис. 1 Распределение давления на передних и
задних поверхностях лезвия резца
На величину и направление силы резания влияет ряд факторов процесса резания. При этом для каждого процесса существует свой логически обоснованный вариант разложения силы резания на составляющие. В частности, при анализе точения силу резания раскладывают на три взаимно перпенди кулярных направления (рис. 3). В этой системе Рг представляет собой окружную силу, которую считают главной составляющей силы резания. Она действует в направлении траектории главного движения. Обычно по ее величине определяют мощность резания N и крутящий момент М:
N = PZ V /6x104;
М=PZD/2000,
где D - диаметр обтачиваемой поверхности, мм; V - скорость резания, м/мин.

Рис. 2 Составляющие силы резания при точении
По силе Рк рассчитывается на прочность механизм подачи станка. Ру - радиальная сила, направленная нормально к обрабатываемой поверхности. По силам Ру и Pz рассчитывается деформация обрабатываемой детали и
узлов станка, что в значительной степени влияет на точность и качество обработанной поверхности.
Составляющие силы в нормальных условиях резания, как правило, имеют соотношение:
Рк = (0,2 ÷ 0,3) Pz ;
Ру = (0,3 ÷ 0,4) Рг.
Устройства для сбора опытных данных. В случае резания по методу токарной обработки величину сил, составляющих силу резания, измеряют специальными динамометрами, встраиваемыми в линию действия измеряемой силы. Динамометры могут быть:
- трехкомпонентными (для измерения составляющих Pz, Ру, Рx );
- двухкомпонентными (для измерения Pz и Ру или Pz и Рx);
- однокомпонентными (обычно для измерения Рг).
В состав каждого динамометра входят:
а) устройства для разложения равнодействующей силы резания на составляющие;
б) датчики, служащие для преобразования измеряемой силы в удобно наблюдаемую величину;
в) регистрирующее устройство.
В зависимости от принципа действия датчики бывают электрическими, гидравлическими или упругими. В настоящее время наиболее распространены электрические датчики, которые бывают следующих видов.
1) Датчики сопротивления (тензометры), в которых используется свойство проводника электрического тока изменять свое омическое сопротивление при изменении внутреннего напряжения или площади поперечного сечения под действием измеряемой силы. Индуктивные датчики, основанные на использовании изменения индуктивного сопротивления катушки при изменении зазора или механического напряжения под действием измеряемой силы.
2) Емкостные датчики, способные регистрировать изменение зазора между пластинами конденсатора, одна из которых упруго деформируется под действием внешней измеряемой силы.
3) Пьезоэлектрические датчики, основанные на свойстве кристаллов кварца, турмалина или сегнетовой соли образовывать на поверхности электрические заряды под действием внешней силы.
Принципиальная схема тензоэлектрического измерительного устройства показана на рис. 3.

Рис. 3 Схема измерения силы резания
тензоэлектрическим динамометром
На
упругий измеритель элемент 1 подвергаемый воздействию силы  наклеен
тензометрический датчик 2. Для измерения сопротивления датчика используется
мостовая схема из сопротивлений RI, R2, R3 и R4, в которую датчик сопротивлением R1 подсоединяется в качестве одного
из плеч моста. Упругая деформация измерительного элемента 1 и, соответственно,
наклеенного на нем датчика вызывает изменение сопротивления R1. Этим нарушается баланс моста,
питаемого напряжением от источника 3. Возникает разность потенциалов между
точками А и В моста. Изменение сопротивления R1 пропорционально деформации упругого
элемента под действием силы
наклеен
тензометрический датчик 2. Для измерения сопротивления датчика используется
мостовая схема из сопротивлений RI, R2, R3 и R4, в которую датчик сопротивлением R1 подсоединяется в качестве одного
из плеч моста. Упругая деформация измерительного элемента 1 и, соответственно,
наклеенного на нем датчика вызывает изменение сопротивления R1. Этим нарушается баланс моста,
питаемого напряжением от источника 3. Возникает разность потенциалов между
точками А и В моста. Изменение сопротивления R1 пропорционально деформации упругого
элемента под действием силы  . Усилитель 4, подсоединенный
к точкам А и В моста, усиливает сигнал разбаланса, который затем поступает на
регистрирующий прибор 5. Отклонение Н на ленте 6, зафиксированное при резании,
можно пересчитать в значение действующей при резании составляющей силы резания Рг согласно данным тарировки.
. Усилитель 4, подсоединенный
к точкам А и В моста, усиливает сигнал разбаланса, который затем поступает на
регистрирующий прибор 5. Отклонение Н на ленте 6, зафиксированное при резании,
можно пересчитать в значение действующей при резании составляющей силы резания Рг согласно данным тарировки.
Среди динамометров с электрическими датчиками наиболее распространен централизованно выпускаемый универсальный динамометр (УДМ) Е.Н. Мухина. Он позволяет измерять три составляющие силы резания при точении, фрезеровании, а также осевую силу и крутящий момент при сверлении, зенкеровании и т.д.
Если, например, при точении необходимо определить зависимость от режимов резания только главной составляющей силы резания, то целесообразно воспользоваться однокомпонентным динамометром ДК-1 (рис. 4). Динамометр устанавливают на верхних салазках суппорта токарного станка вместо предварительно снятого резцедержателя и закрепляют болтом, проходящим сквозь отверстие А. Резец закрепляют в державке 3, которая соединена с корпусом динамометра 1 двумя торсионными брусками 2.
Под действием силы Pz резец слегка отжимается вниз, закручивая торсионные бруски. При этом находящийся в нижней части прибора конец планки 7, приваренной к державке 3, поднимается, нажимая стержнем 6 на ножку индикатора 5. Перемещение ножки индикатора пропорционально деформации торсионных брусков и. следовательно, вертикальной составляющей силы Рг. Цена деления индикатора определяется предварительной тарировкой.
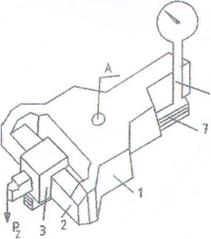
Рис.4 Конструкция однокомпонентного динамометра ДК-1
Сущность методики испытаний. Посредством испытаний стремятся установить связь между силой резания и основными параметрами, совокупность которых охватывает понятие режим резания.
В том случае, когда для измерения
силы используют простейший однокомпонентный динамометр, а в числе переменных
параметров включены только глубина резания t, подача S и скорость резания v, суть методики испытании сводится к
следующему. Последовательно изменяют величину одного параметра (например /), а
два других (например v и S) оставляют постоянными для
серии измерений силы резания. В результате получают набор экспериментальных
данных для построения графиков в координатах Рг (РХ, Ру) =  (t); Рг (РХ ,
Ру) =
(t); Рг (РХ ,
Ру) =  (S); Рг (РХ, Ру) =
(S); Рг (РХ, Ру) =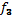 (V).
(V).
Обработка результатов испытаний. Характерной особенностью полученных графических зависимостей является то, что по своей конфигурации графики близки к теоретическим кривым, имеющих математические уравнения типа
y = В х п,
где B и n - численные коэффициенты.
Это обстоятельство послужило основанием для аппроксимации экспериментально получаемых графиков математическими зависимостями:
Рг =  ×
×  при V, S-const;
при V, S-const;
Рг= С"рг ×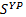 при V, t- const; Рг =
при V, t- const; Рг =  рг ×
рг × при S, t – const
при S, t – const
Набор этих графиков представлен на рис. 5. Процедура вычисления коэффициентов Cpz и показателей степеней X, У, n таких функций существенно упрощается после логарифмирования, что наглядно иллюстрируется видом получаемых степенных функций в логарифмических координатах (рис. 6):
In Рг = In +
 In
t;
In
t;
In Рг = In С"рz +  InS;
InS;
In Рг= In  +
+ 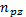 In V.
In V.

Рис. 5 Зависимости составляющих силы резания Рг (Py Рг )
от режимов резания t, S, V
Полученные уравнения аналогичны уравнениям первой степени вида
V = а + b X.
В
этих уравнениях показатели степеней  ,
,  ,
, 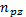 функционально отражают влияние
на силу резания таких параметров, как t, S и V, а численно они равны
тангенсам угла наклона линий Рг=
функционально отражают влияние
на силу резания таких параметров, как t, S и V, а численно они равны
тангенсам угла наклона линий Рг= (t); Рг = f 2 (S); Р2 =
(t); Рг = f 2 (S); Р2 = 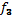 (V) к горизонтальной оси (рис. 6):
(V) к горизонтальной оси (рис. 6):
 Хрz = tg
Хрz = tg ;
;  = tga2;
= tga2; 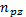 = tgα3.
= tgα3.

Соответственно
коэффициенты , ,
, , предопределяются материалом
заготовки и инструмента, условиями обработки и прочими факторами режима
резания, а численно равны составляющей
, предопределяются материалом
заготовки и инструмента, условиями обработки и прочими факторами режима
резания, а численно равны составляющей  при единичных значениях V, S, t(V= 1 м/мин; S = 1 мм/об, t = 1 мм). На графиках
зависимостей
при единичных значениях V, S, t(V= 1 м/мин; S = 1 мм/об, t = 1 мм). На графиках
зависимостей  =f{V, S, t) коэффициент
=f{V, S, t) коэффициент  оценивается
величиной отрезка, отсекаемого прямой этих зависимостей на осях координат (рис.
6).
оценивается
величиной отрезка, отсекаемого прямой этих зависимостей на осях координат (рис.
6).
Формирование математической модели. На основании обработки экспериментальных данных с учетом графоаналитического анализа установлено, что составляющие силы резания, например, при точении могут быть вычислены по следующим уравнениям:
 =×
=× ×
×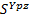 ×
× ×
× ;
;
Рх = СРх
× tХрх × SYpx ×  ×
× ;
;
PY = СРy
× tХру × SYpy × 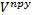 ×
× ,
,
где  СРy , СРх -
постоянные коэффициенты, зависящие от физико-механических свойств материала
заготовки и условий обработки;
СРy , СРх -
постоянные коэффициенты, зависящие от физико-механических свойств материала
заготовки и условий обработки;  , ,
, ,  ,
,  ,
,  , ХРx,
, ХРx, 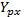 ,
, - показатели степеней, учитывающие влияние режимов резания:
- показатели степеней, учитывающие влияние режимов резания:
Крх, Кру, КрZ - поправочные коэффициенты, учитывающие изменение условий резания, по сравнению с нормативными.

Рис. 6 Зависимости составляющих силы резания  (Ру, Рх)
(Ру, Рх)
от режимов резания t, S, V в логарифмических координатах
Система уравнений (2.17) представляет собой матемаггоческую модель резания, опирающуюся на крупный массив предварительных экспериментальных работ, что. в свою очередь, связано с крупными производственными затратами.
Основное достоинство этой математической модели в том, что установлена математическая связь между силой резания и основными параметрами: глубиной резания, подачей и скоростью резания. Тем более что процесс обработки резанием начинают, предварительно назначив t и S, а для скорости резания отдельно сформирована эмпирическая зависимость типа
v =  /
/ 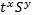 ,
,
где Су - табличный коэффициент, характеризующий обрабатываемый материал при определенных условиях работы; х, у - табличные показатели степени, численные значения которых установлены для каждой группы обрабатываемых материалов при конкретных диапазонах изменения глубины резания t и подачи S.
На основании уравнения (2.19) при назначенных величинах / и S предварительно вычисляют скорость резания. Это найденное значение скорости является ориентировочным, и его используют для прикидочного вычисления требуемого числа оборотов п инструмента или детали (в зависимости от способа резания). Например, как уже упоминалось, при токарной обработке скорость резания
v = π D п/ 1000, откуда п = 1000 v/πD
Полученное число п сверяют с имеющимся набором чисел оборотов станка, на котором будет реализовываться резание. Выбрав число оборотов, ближайшее к расчетному, обратным вычислением уточняют скорость, которая будет иметь место при резании, и это же значение скорости используют в уравнениях (2.17) для вычисления силы резания.
В перечень недостатков системы уравнений (2.17) входят:
а) уравнения, составляющие эту математическую модель, не имеют физического смысла;
б) расчет силы резания отягощен большим объемом рутинной работы. связанной с необходимостью выбирать по таблицам справочников большое количество численных значений коэффициентов и показателей степени;
в) результат вычисления по уравнениям (2.17), в конечном счёте, даёт весьма приблизительное значение силы резания по целому ряду причин. Основные причины следующие.
1) Сама по себе аппроксимация, то есть приближение экспериментального графика к теоретическому графику, имеющему математическое описание в виде степенной зависимости, сопровождается вполне конкретным несовпадением сближаемых кривых. Несовпадение графиков оценивается величиной погрешности, которая даже в первом приближении может выходить за пределы, приемлемые для инженерных расчётов.
2) Дополнительные погрешности вносит методика графоаналитических построений уравнения.
3) Очень большое число таблично представленных коэффициентов при грубо упрощённой классификации как материалов инструмента (типа «твёрдый сплав», «быстрорежущая сталь»), так и обрабатываемых материалов (типа «сталь», «чугун»).
Наличие дополнительных коэффициентов, характеризующих взаимно связанные показатели: коэффициент, учитывающий износ инструмента; коэффициент, учитывающий стойкость инструмента; коэффициент, учитывающий, например, величину главного угла в плане резца, хотя этот угол по своей сути предопределяет длину участка лезвия, непосредственно участвующей в резании, а лезвие, в свою очередь, подвергается износу.
Несмотря на указанные недостатки, эта математическая модель наиболее часто реализуется в инженерной практике. Это объясняется тем, что погрешность расчета силы резания компенсируют повышением запаса конструктивной прочности режущего инструмента, электродвигатель станка берут с несколько завышенной мощностью, а также реализуют ряд других конструкторско-технологических приемов. То есть неточность расчетов по сформированной математической модели компенсируют бесплодным завышением количества энергии, вводимой в процесс резания.
Список литературы
1. Резание материалов И.А.Чечета, В.И.Гунин, О.Н. Кириллов
2. Справочник технолога машиностроителя А.Г.Косилова














 (zip - application/zip)
(zip - application/zip)










