доклада Изгиб

Департамент внутренней и кадровой политики Белгородской области Областное государственное автономное образовательное учреждение «Корочанский сельскохозяйственный техникум»

Реферат:

По дисциплине «Техническая механика»

Тема доклада «Изгиб»

Работу выполнил студентка 31-т группы

Специальности «Технология производства и переработки с/х продукции»

Ломонос Елена Михайловна

Проверил:

Преподаватель Бакланов Дмитрий Александрович

Короча 2020

Содержание

1. Общие сведения и основные определения .

2.Дифференциальные зависимости при поперечном изгибе .

3.Напряжение при чистом изгибе .

4.Касательное напряжение при поперечном изгибе. Формула Журавского .

5.Расчеты на прочность при изгибе .

6.Определение перемещений при изгибе. Дифференциальное уравнение изогнутой оси балки .

7. Теорема о взаимности работ. Теорема о взаимности перемещений .

 8.Определение перемещений методом Мора .

Литература

1.Общие сведения и основные определения

Весьма часто в технике стержни подвергаются действию поперечной нагрузки и изгибающих моментов. При этом в поперечных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня, и поперечные силы. При действии такой нагрузки ось стержня искривляется. Указанный вид нагружения называется изгибом, а стержни, работающие на изгиб, принято называть балками.
(5.1)

Этот вид деформаций принято называть изгибом в двух плоскостях или косым изгибом. Косой изгиб в соответствии с принципом суперпозиции эквивалентен совокупности двух плоских изгибов.
(5.2)

Изгиб называют чистым, если изгибающий момент является единственным внутренним силовым фактором, возникающим в поперечном сечении балки.
(5.3)

Чаще, однако, в поперечных сечениях наряду с изгибающим моментом возникают также и поперечные силы. Такой изгиб называют поперечным.

 Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных осей поперечного сечения стержня, изгиб носит название простого или плоского. В последнем случае применяется также название прямой изгиб.
Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, то изгиб называют косым. При плоском изгибе ось балки и после деформации остается в плоскости внешних сил - силовой плоскости. При косом изгибе плоскость деформации не совпадает с силовой плоскостью.

 Для построения эпюр внутренних силовых факторов может быть использован метод сечений (см. раздел 1.5). Простейший пример построения эпюр внутренних силовых факторов при изгибе приведен на рис. 5.1

Рис. 1. Построение эпюр внутренних силовых факторов при изгибе

 Последних 200-300 лет развития техники связаны с использованием конструкций, работающих на изгиб. Это придает современным конструкциям легкий, изящный облик.

2. Дифференциальные зависимости при поперечном изгибе  

 Выделим на балке бесконечно малый элемент

Рис. 2. Выделение бесконечно малого элемента при изгибе

 Установим связь между внутренними силовыми факторами и внешней нагрузкой. С этой целью используем уравнение равновесия в проекциях сил на вертикальную ось Оу

(5.4)

В соответствии с (5.4) знак тангенса угла наклона в эпюре  совпадает со знаком погонной нагрузки . Если  положительна, то производная «+» и величина перерезывающей силы  будет с увеличением  будет возрастать. Если  отсутствует, то производная равна 0 и перерезывающая сила  будет оставаться постоянной. И наконец, если  отрицательна, то производная «-» и величина перерезывающей силы  будет с увеличением  будет уменьшаться.
 Используем еще одно уравнение равновесия в проекциях моментов на ось, перпендикулярную плоскости чертежа Ох (относительно точки 1)

В этом выражении оставим только величины первого порядка малости (5.5)

(5.5)

Наконец, после подстановки (5.5) в (5.4) можно получить
(5.6)

Зависимость (6.6) обосновывает возможность использования «правило зонтика».

Рис. 3. Использования знака кривизны для проверки правильности построения эпюр внутренних силовых факторов при изгибе

Таким образом, эпюры внутренних силовых факторов   и  при изгибе связаны интегрально-дифференциальными зависимостями.

3.Напряжение при чистом изгибе

Пользуясь принципом суперпозиции, часто встречающийся в технических приложениях поперечный изгиб разложим на 2 случая:

. чистый изгиб; .

действие одной перерезывающей силы.

И для случая чистого изгиба может быть использована гипотеза Бернулли.

Рис 4. Выделение бесконечно малого элемента для чистого изгиба (н.л. - нейтральная линия)

При изгибе нижние волокна сжимаются, верхние - растягиваются, среднее волокно или нейтральная линия не деформируется.

 Непосредственно их рис 5.4.

Используем закон Гука
(5.7)

Для заданного сечения

Используем уравнение равновесия. Рассмотрим равновесие всех сил, действующих в некотором сечении общего вида

Рис. 5. К выводу уравнений равновесия при изгибе

Общее число уравнений равновесия шесть:

·   три - в силах, ·

   три - в моментах.

Некоторые из этих уравнений равновесия представляют собою тождества º 0.

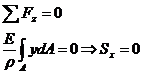
(5.8)

Зависимость (5.8) может быть в дальнейшем использована для оценки деформаций конструкции. После подстановки (5.8) в (5.7)

Используя  - осевой момент сопротивления.

(5.9)

4. Касательное напряжение при поперечном изгибе. Формула Журавского

Нормальное напряжение при поперечном изгибе определяется как при чистом изгибе по формуле (5.9) и в настоящем разделе рассмотрим в соответствии с принципом суперпозиции только действие поперечной силы

Рис. 6. Определение касательных напряжений при поперечном изгибе

Действующие нормальные напряжения на боковых гранях выделенного бесконечно малого элемента равны

 

Спроектируем все силы на ось Z.

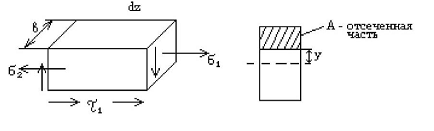
Рис 7. Равновесие отсеченной части балки при поперечном изгибе

S"x - статический момент отсеченной части поперечного сечения.

(5.10)

На рис. 5.8. приведены примеры распределения касательных напряжений для некоторых поперечных сечений бруса.

Рис 8. Эпюры касательных напряжений при поперечном изгибе Формула Журавского имеет значение для тонкостенной конструкции.

5. Расчеты на прочность при изгибе

 По аналогии с другими ранее изученными видами напряженных и деформированных состояний можно выделить три вида расчеты на прочность при изгибе: 

5.1. Проектировочный расчет. В этом случае при известных внешних нагрузках с помощью метода сечений строятся эпюры внутренних силовых факторов - поперечных сил и изгибающих моментов. Для максимального изгибающего момента   при известных допускаемых напряжениях  можно определить необходимый с позиций обеспечения прочности момент сопротивления
 

По известному моменту сопротивления можно определить номер прокатной стали или характерный геометрической размер поперечного сечения заданного типа.

.2. Проверочный расчет. И вновь при известных внешних нагрузках с помощью метода сечений строятся эпюры внутренних силовых факторов - поперечных сил и изгибающих моментов. Для максимального изгибающего момента   при заданном поперечном сечении, то есть известном моменте сопротивления , можно  определить максимальные нормальные напряжения

Для проверки прочности достаточно вычислить коэффициент запаса прочности

Если этот коэффициент больше единицы, то сохраняется работоспособное состояние.

 .3. Определение предельной нагрузки. В большинстве практических случаев максимальный изгибающий момент может быть представлен в следующем виде

где  - некоторый числовой коэффициент, зависящий от конструктивной схемы балки, от способа ее нагружения и от граничных условий. Тогда справедлива следующая зависимость для предельной нагрузки

6. Определение перемещений при изгибе. Дифференциальное уравнение изогнутой оси балки

 Для качественной оценки вида изогнутой оси балки можно использовать следующую зависимость:

Если,  т.е.  , то это прямолинейный участок.   Знак кривизны совпадает со знаком изгибающего момента.

Рис. 9. Знаки кривизны упругой линии и изгибающего момента

 Для достаточно гладких функций в математике и для малой деформации в технической механике справедлива следующая зависимость.

(5.11)

гдеV - линейное перемещение по оси Oу или прогиб.

 Выражение (5.11) в механике деформируемых твердых тел известно, как дифференциальное уравнение изогнутой оси балки. Уравнение (5.11) оказывается справедливым только для отдельного участка балки, в пределах которого вся правая часть имеет вид гладкой аналитической функции.

 Рассмотрим случай, когда на балке имеется всего 1 участок.

Рис 10. К определению функции изогнутой оси балки

Исходное дифференциальное уравнение может быть для рассматриваемого случая записано в следующем виде
(5.12)

После интегрирования получаем выражение для функции углов поворота
(5.13)

После еще одного интегрирования получаем выражение для функции прогиба

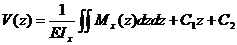(5.14)

Для определение постоянных интегрирования   и   рассмотрим граничные условия в жесткой заделке
  граничные условия.

Если мы имеет N участков, то нам неизвестно 2N постоянных интегрирования. Кроме граничных условий мы должны использовать условия сопряжения.

Рис 11. Балка, содержащая два участка

Пример 5.1. Рассмотрим методику интегрирования дифференциального уравнения упругой линии консольной балки

Рис. 12. Определений перемещений при изгибе консольной балки

(5.14)

Использование дифференциального уравнения изогнутой оси балки (5.10) при большом количестве участков связано с определенными вычислительными трудностями.

7. Теорема о взаимности работ. Теорема о взаимности перемещений.

Рассмотрим линейно-деформируемую систему в двух различных состояниях, отвечающих двум различным нагрузкам (рис. 5.15).Для простоты выкладок рассмотрим простую двухопорную балку, последовательно нагружаемую двумя сосредоточенными силами.
 

Рис 15. Прямой и обратный порядок приложения нагрузки

Приравнивая полные работы при прямом и обратном порядке приложения нагрузок, получим
 

Работа , фактически совершаемая силой на перемещениях, вызываемых другой силой или силами, называется дополнительной работой.

Согласно теореме о взаимности работ, работа сил первого состояния на перемещение второго состояния равна работе сил второго состояния на перемещение первого состояния.

 Аналогичным образом может быть доказана также взаимность дополнительной работы внутренних сил.
 

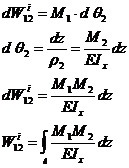
Рис 16. Взаимность дополнительной работы внутренних сил.

 Используя закон сохранения энергии, можно показать, что дополнительная работа внешних сил равна по абсолютному значению дополнительной работе внутренних сил:

(5.16)

Это соотношение будет использовано далее для обоснования общего метода определения перемещений (метода Мора).

Принимая

получим теорему о взаимности перемещений.

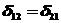(5.17)

Перемещение точки приложения единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки, приложения второй единичной силы по направлению последней, вызванному действием первой единичной силы.

8. Определение перемещений методом Мора

 Вместо системы сил F1 и F2,введем грузовое  и вспомогательное состояния:

Рис 17. Введение грузового и вспомогательного состояний

 Запишем теорему о взаимности работ для этих двух состояний:

После суммирования по отдельным участкам балки получим интеграл Мора

(5.18)

Пример 5.2. Рассмотрим пример на использование интеграла Мора на определение перемещений для консольной балки, нагруженной сосредоточенной силой

Рис 18. Построение грузовой и вспомогательной эпюры для консольной балки

Используем интеграл Мора

На практике использование такого подхода затруднено. Эта трудность преодолевается организацией интегрирования, интегрирование легко реализуется на компьютере.

Литература

1. •Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. 7-е изд. - М.: Высшая школа, 2009. - 560 с. Посмотреть•Алмаметов Ф. 3., Арсеньев С: И., Курицын Н. А., Мишин А. М. Расчет­ные и курсовые работы по сопротивлению материалов. - М.: Высшая школа, 2003. - 367 с.

 2. •Биргер И. А., Мавлютов P.P. Сопротивление материалов.- М.: Наука, 1986. -560 с. .    •Бондаренко А.Н. Курс лекций по сопротивлению материалов - МИИТ, 2007 Посмотреть•Сопротивление материалов, Н. М. Беляев, Главная редакция физико-математической литературы изд-ва «Наука», 1976 г., стр. 608. .   

•Механика разрушения и прочность материалов. Справочное пособие в 4-х томах. - Киев.: Наукова думка, 1988. - 2000 с. .   

 •Миролюбов И. Н. и др. Пособие к решению задач по сопротивлению материалов. - М.: Высшая школа, 1985. - 400 с. .   

•Макаров Е.Г. Сопротивление материалов на базе marhcad. - СПб.: БХВ-Петербург, 2004. - 512 с.: ил. Приобрести•Писаренко Г. С, Яковлев А. П., Матвеев В. В. Справочник по сопротив­лению материалов. - Киев.: Наука, 1975. - 400 с. .   

•Порошии И.Б. Расчеты на прочность - это просто!: Учебное пособие. -Челябинск: ЮУрГУ, 2005. - 44 с. •Работнов Юрий Николаевич. Сопротивление материалов. М., Физматгиз. 1962 г., 456 стр. с илл .  

•Сопротивление материалов / Под ред. А. Ф. Смирнова.- М.: Высшая школа, 1975. -480 с. .   

 •Сурьянинов Н.Г. Методы построения эпюр в статически определимых и статически неопределимых системах - 2001, 155с.