Содержание
Задание №1……………………………………………………………3
Задание №2……………………………………………………………4
Задание №3……………………………………………………………5
Задание №4……………………………………………………………6
Задание №5……………………………………………………………7
Задание №6……………………………………………………………9
Задание №7……………………………………………………………10
Задание №8……………………………………………………………11
Задание №9……………………………………………………………12
Задание №10…………………………………………………………..15
Задание №11…………………………………………………………..19
Задание №12…………………………………………………………..21
Список литературы…………………………………………………...24
Задание №1
Система состоит из 6 независимых работающих элементов. Вероятность отказа элемента равна 0,3. Найти вероятность отказа системы, если для этого достаточно, чтобы отказали, хотя бы пять элементов.
Решение:
А = {элемент откажет}.
q = 1 – p = 1 – 0,3 = 0,7
События независимые.
Применим формулу Бернулли.
,
где 
0,0102
+ 0,0007 = 0,0109
Ответ: Вероятность отказа системы равна 0,0109.
Задание №2
Известно, что вероятность выпуска дефектной детали равна 0,02. Детали укладываются в коробки по 100 штук. Чему равна вероятность того, что: а) в коробке нет дефектных деталей; б) число дефектных деталей не более двух?
Решение:
А = {деталь дефектная}.
События независимые.
Применим формулу Пуассона.
а) 
б) 
= 0,1353 + 0,2707 + 0,2707 = 0,6767
Ответ: Вероятность того, что в коробке: а) нет дефектных деталей, равна 0,1353; б) число дефектных деталей не более двух равна 0,6767.
Задание №3
Среди семян ржи имеется 0,2% сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить не более 3 семян сорняков?
Решение:
А = {обнаружен сорняк}.
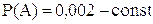
События независимые.
Применим формулу Пуассона.
0,00005 +
0,00045 + 0,00227 + 0,00757 = 0,01034
Ответ: Вероятность того, что при случайном отборе 5000 семян будет обнаружено не более 3-х семян сорняков, равна 0,01034.
Задание №4
Вероятность появления успеха в каждом испытании равна 0,4. Найти вероятность того, что при 550 испытаниях успех наступит не менее 210 и не более 240 раз.
Решение:
А = {наступление успеха в одном испытании}.
q = 1 – p = 1 – 0,4 = 0,6
События независимые.
Применим интегральную теорему Муавра-Лапласа.
=
= Ф(1,74) – Ф(–0,87) = Ф(1,74) + Ф(0,87) = 0,4591 + 0,3078 = 0,7669
Ответ: Вероятность того, что при 550 испытаниях успех наступит не менее 210 и не более 240 раз равна 0,7669.
Задание №5
Две радиолокационные станции ведут наблюдение за областью
пространства, в которой перемещается объект, в течение времени 
. За это время
первая станция успевает произвести 2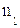
циклов
обзора, вторая – 2
циклов. За
один цикл обзора первой станцией объект обнаруживается (независимо от других) с
вероятностью 
, второй – с
вероятностью 
. Найти вероятность
событий: А = {объект обнаружен за время хотя бы одной из
станций}; В = {объект обнаружен первой станцией и не обнаружен второй}; С =
{объект не обнаружен за первую половину времени , но обнаружен за
вторую}.
Решение:
1. А = {объект обнаружен за время хотя бы одной из
станций}.
=
{объект не обнаружен за время ни
одной из станций}.
Р(А) = 1 – Р()
=
{объект не обнаружен за время первой
станцией}.
=
{объект не обнаружен за время второй
станцией}.
Р()
= 
Р()
= 
P() = Р()∙Р() = 
∙
P(A) = 1 – ∙
2. В = {за время объект обнаружен первой
станцией и не обнаружен второй}.
Р(В) = Р(
)∙Р() = (1 – )∙
3. С = {объект не обнаружен за первую половину
времени , но обнаружен за
вторую}.
=
{объект не обнаружен за первую половину времени }.
=
{объект обнаружен за вторую половину времени }.
Р()
=
∙
Р()
= 1 – ∙
Р(С) = Р()∙Р() = ∙∙(1 – ∙)
Ответ: Вероятность того, что:
1. за время объект будет
обнаружен одной из станций, равна
1 – ∙;
2. за время объект будет
обнаружен первой станцией и не обнаружен второй, равна (1 – )∙;
3. объект не обнаружен за первую половину времени
, но обнаружен за
вторую, равна ∙∙(1 – ∙).
Задание №6
В коробке 6 красных и 4 синих карандаша. Наугад вытаскиваются три из них. Найти вероятность событий: А = {вытащены карандаши одного цвета}; В = {вытащены хотя бы два красных карандаша}.
Решение:
Общее число равновозможных исходов испытания:
n = 
120.
1. А = {вытащены карандаши одного цвета}.
Число благоприятных для события А исходов испытания:
m = 
Искомая вероятность:
2. В = {вытащены хотя бы два красных карандаша}.
Число благоприятных для события В исходов испытания:
m = 
Искомая вероятность:
Ответ: Вероятность того, что среди наугад выбранных трех карандашей:
1. все одного цвета, равна 0,2;
2. хотя бы два красных карандаша, составит 0,6667.
Задание №7
Слово МАТЕМАТИКА разрезается на буквы. Буквы перемешиваются и снова складываются слева направо. Найти вероятность того, что снова получится слово МАТЕМАТИКА.
Решение:
С = {получится слово МАТЕМАТИКА}.
Р(С) = Р(МАТЕМАТИКА) = Р(М)∙
∙
∙
∙
∙
∙
∙
∙
∙
∙
Р(С) =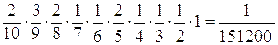 
=
0,000007
Ответ: Вероятность того, что получится слово МАТЕМАТИКА, равна 0,000007.
Задание №8
В бригаде 8 рабочих и 2 ученика. Вероятность изготовить бракованное изделие для рабочего составляет 0,05, для ученика 0,2. Производительность рабочего в два раза выше, чем у ученика. Какова вероятность, что некоторое изделие, изготовленное бригадой, окажется бракованным?
Решение:
Е = {изделие бракованное};
=
{изделие изготовлено рабочим};
=
{изделие изготовлено учеником}.
Определим Р(Е), используя формулу полной вероятности.
Ответ: Вероятность того, что некоторое изделие, изготовленное бригадой, окажется бракованным, равна 0,0667.
Задание №9
Дискретная случайная величина Х задана таблицей:
|
|
1 |
2 |
4 |
6 |
8 |
9 |
10 |
|
|
0,05 |
0,10 |
0,30 |
0,20 |
0,10 |
0,20 |
0,05 |
1) Убедитесь, что задан ряд распределения.
2) Найдите функцию распределения случайной величины Х и постройте ее график.
3) Найдите Р(2 ≤ х < 9).
4) Найдите математическое ожидание, дисперсию, среднее квадратическое отклонение, начальный момент третьего порядка, центральный момент третьего порядка для заданной случайной величины Х.
Решение:
1) Убедимся, что задан ряд распределения.
=
0,05 + 0,10 + 0,30 + 0,20 + 0,10 + 0,20 + 0,05 = 1, следовательно, задан ряд
распределения случайной величины Х.
2) Определим функцию распределения случайной величины Х и построим ее график.
F(х) = P(X < x)
3) Найдем Р(2 ≤ х < 9).
Р(2 ≤ х < 9) = Р(х = 2) + Р(х = 4) + Р(х = 6) + Р(х = 8) = 0,10 + 0,30 +
+ 0,20 + 0,10 = 0,70
4) Определим:
а) математическое ожидание.
M(x) = 
M(x) = 1∙0,05 + 2∙0,10 + 4∙0,30 + 6∙0,20 + 8∙0,10 + 9∙0,20 + 10∙0,05 = 5,75
б) дисперсию.
D(x) = 
D(x) = 
+ 
6,9875
в) среднее квадратическое отклонение.
=
2,64
г) начальный момент третьего порядка.
=
∙0,05 + 
∙0,10 + 
∙0,30 + 
∙0,20 + 
∙0,10 + 
∙0,20 +
+ 
∙0,05
= 310,25
д) центральный момент третьего порядка.
=
=
+ 
= – 0,3938
Ответ: ;
Р(2 ≤ х < 9) = 0,70; М(х) = 5,75; D(x) = 6,9875; 
;
=
310,25; = – 0,3938.
Задание №10
Непрерывная случайная величина Х подчинена закону распределения с плотностью:
Найти:
1) коэффициент а;
2) математическое ожидание, дисперсию, среднее квадратическое отклонение, начальный момент третьего порядка для заданной случайной величины Х.
3) найти вероятность попадания случайной величины Х
в промежуток 
.
Решение:
1) Определим коэффициент а.
+
+
= 1
=
1
=
1
=
1
a = 1
Тогда
2) Определим:
а) математическое ожидание.
M(x) = + 
+ = = 
=
=
–
+ 
= 
б) дисперсию.
D(x) = + 
+ 
= =
= 
=
–
= 
= 
+
+ 
–
= 
– 
– + 
– 1 – 
= – 1–
– 2 = –
3
в) среднее квадратическое отклонение.
г) начальный момент 3-го порядка.
=
=
+ 
+ = = 
=
= 
–
= 
= 
+ 
– 
=
= 
= 
– 
+ 
= – 
– 
=
= – 
+ 6
5) Определим Р
P(a < x < b) =
P = 
+ 
= = 
= 
– 
= 1 –
– 
= 0,1340
Ответ: а = 1; M(x) = ; D(x) = – 3; = = – + 6;
P = 0,1340; 
.
Задание №11
По следующим данным составить вариационный ряд, найти выборочную среднюю, исправленную выборочную дисперсию, исправленное среднее квадратическое отклонение, ошибку средней, выборочный коэффициент вариации.
|
30 |
39 |
32 |
27 |
36 |
32 |
34 |
26 |
23 |
28 |
Решение:
1) Составим вариационный ряд.
|
|
23 |
26 |
27 |
28 |
30 |
32 |
34 |
36 |
39 |
|
|
1 |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
2) Определим выборочную среднюю.
30,7
3) Определим исправленную выборочную дисперсию.
= 21,41
23,79
4) Определим исправленное среднее квадратическое отклонение.
= 4,88
5) Определим ошибку средней.
6) Определим коэффициент вариации.
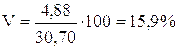
Ответ: 
30,7;
; S = 4,88; 
; V = 15,9%.
Задание №12
Имеются следующие данные для случайных величин X и Y:
|
|
87 |
92 |
93 |
101 |
104 |
94 |
98 |
85 |
99 |
95 |
|
|
58 |
62 |
60 |
71 |
64 |
59 |
61 |
49 |
56 |
65 |
1) Найти выборочный коэффициент корреляции и сделать выводы о тесноте и направленности линейной корреляционной связи между X и Y.
2) Составить выборочное уравнение прямой регрессии Y на Х.
3) Нанести на чертеж исходные данные и полученное уравнение регрессии.
Решение:
1) Определим выборочный коэффициент корреляции.
Промежуточные расчеты представим в табл. 1.
Таблица 1
|
№ п/п |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
87 |
58 |
7569 |
5046 |
3364 |
55,4 |
|
2 |
92 |
62 |
8464 |
5704 |
3844 |
58,7 |
|
3 |
93 |
60 |
8649 |
5580 |
3600 |
59,3 |
|
4 |
101 |
71 |
10201 |
7171 |
5041 |
64,6 |
|
5 |
104 |
64 |
10816 |
6656 |
4096 |
66,6 |
|
6 |
94 |
59 |
8836 |
5546 |
3481 |
60,0 |
|
7 |
98 |
61 |
9604 |
5978 |
3721 |
62,6 |
Окончание табл. 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
85 |
49 |
7225 |
4165 |
2401 |
54,0 |
|
9 |
99 |
56 |
9801 |
5544 |
3136 |
63,3 |
|
10 |
95 |
65 |
9025 |
6175 |
4225 |
60,6 |
|
Итого |
948 |
605 |
90190 |
57565 |
36909 |
605 |
|
Средняя |
94,8 |
60,5 |
9019 |
5756,5 |
3690,9 |
– |
Между изучаемыми признаками присутствует прямая и приемлемая по тесноте связь.
2) Составим выборочное уравнение прямой регрессии Y на Х.
=
a + b∙x, где
Отсюда уравнение имеет вид:
=
– 2,087 + 0,660х
С увеличением фактора Х на 1 ед. результат Y увеличится на 0,660 ед.
3) Нанесем на чертеж исходные данные и полученное уравнение регрессии.
Список литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400с.: ил.
2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2006. – 573с.
3. Эконометрика: Учебник /Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344с.: ил.
(zip - application/zip)
Статистика файлового архива
